题目内容
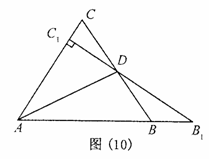
如图(1)所示:等边△![]() 中,线段
中,线段![]() 为其内角平分线,过
为其内角平分线,过![]() 点的直线
点的直线![]() 于
于![]() 交
交![]() 的延长线于
的延长线于![]() .
.
(1)请你探究:![]() ,
,![]() 是否成立?
是否成立?
(2)请你继续探究:若△![]() 为任意三角形,线段
为任意三角形,线段![]() 为其内角平分线,请问
为其内角平分线,请问![]() 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
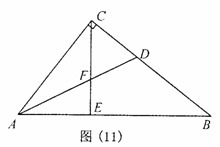
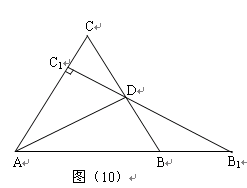
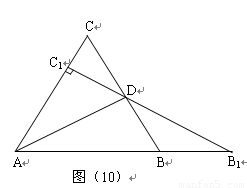
 (3)如图(2)所示
(3)如图(2)所示![]() △
△![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 上一点且
上一点且![]() ,
,![]() 交其内角角平分线
交其内角角平分线![]() 与
与![]() .试求
.试求![]() 的值.
的值.

解:(1)因为ΔABC是等边三角形,所以AB=BC=CA,∠BAC=∠ABC=∠ACB=60°。
又线段![]() 为∠BAC的平分线,∴BD=DC,∠BAD=∠DAC=30°
为∠BAC的平分线,∴BD=DC,∠BAD=∠DAC=30°
∴![]() 。………………………………………………………1分
。………………………………………………………1分
∵![]() ,在RtΔAC1B1中,∠C1AB1=60°,
,在RtΔAC1B1中,∠C1AB1=60°,
则∠B1=30°,AB1= 2A C1……………………………2分
在RtΔAC1 D中,同理:AD=2C1D,又∠B1AD=∠B1=30°∴AD=DB1。
![]() 。这两个等式都成立;………………3分
。这两个等式都成立;………………3分
(2)可以判断结论仍然成立,………………………………4分
证明如下: 如右图所示ΔABC为任意三角形,过B点作BE∥AC交 AD的延长线于E点。
 ∵∠E=∠CAD=∠BAD
∵∠E=∠CAD=∠BAD
∴BE=AB
又∵ΔEBD∽ΔACD ……………………………5分
∴![]()
又∵BE=AB
∴![]() 即对任意三角形结论仍然成立. …………………………6分
即对任意三角形结论仍然成立. …………………………6分
﹙3﹚如图所示,连结ED
∵AD为ΔABC的内角角平分线
∴ ,
,![]() ,即
,即![]() ,
,
又BE=AB-AE=![]() ,得
,得 ……………………7分
……………………7分
 ∴
∴![]() ,又∠B公共,
,又∠B公共,
∴ΔBDE∽ΔBCA……………………8分
∴![]()
∴∠DEB=∠CAB,
∴ DE∥AC
∴ΔDEF∽ΔACF ……………………………9分
∴![]()

练习册系列答案
相关题目
 中,线段
中,线段 为其内角平分线,过
为其内角平分线,过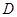 点的直线
点的直线 于
于 交
交 的延长线于
的延长线于 .
.
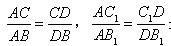 ,是否成立?
,是否成立?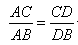 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.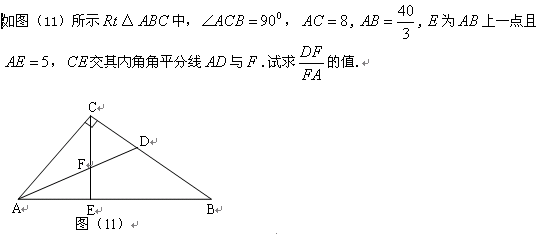
 中,线段
中,线段 为其内角平分线,过
为其内角平分线,过 点的直线
点的直线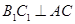 于
于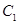 交
交 的延长线于
的延长线于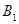 .
.
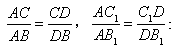 ,是否成立?
,是否成立?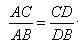 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.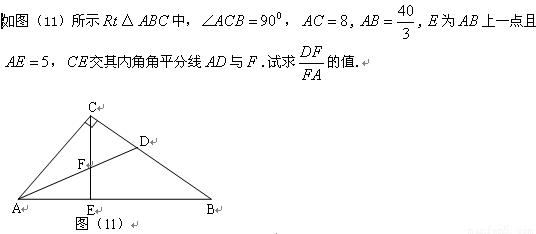
 中,线段
中,线段 为其内角平分线,过
为其内角平分线,过 点的直线
点的直线 于
于 交
交 的延长线于
的延长线于 .
. ,
, 是否成立?
是否成立? 为任意三角形,线段
为任意三角形,线段 为其内角平分线,请问
为其内角平分线,请问 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断. △
△ 中,
中, ,
, ,
, ,
, 为
为 上一点且
上一点且 ,
, 交其内角角平分线
交其内角角平分线 与
与 .试求
.试求 的值.
的值.