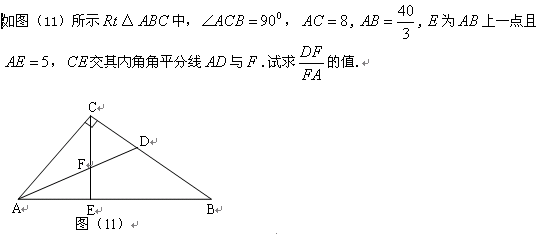
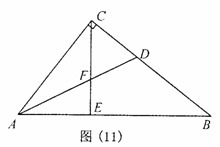
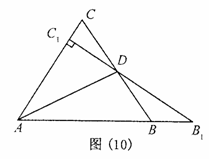
题目内容
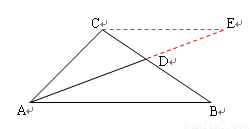
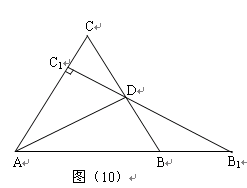
如图(10)所示:等边△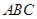 中,线段
中,线段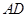 为其内角平分线,过
为其内角平分线,过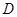 点的直线
点的直线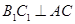 于
于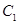 交
交 的延长线于
的延长线于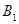 .
.
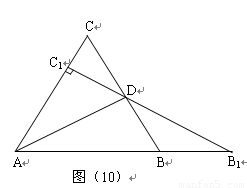
1.请你探究: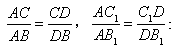 ,是否成立?
,是否成立?
2.请你继续探究:若△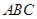 为任意三角形,线段
为任意三角形,线段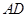 为其内角平分线,请问
为其内角平分线,请问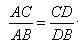 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
3.
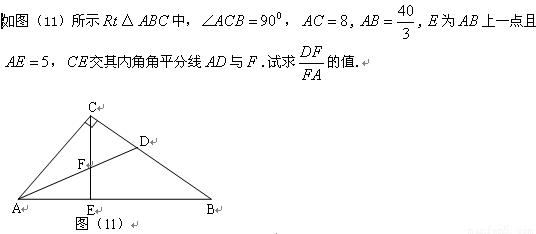
【答案】
1.结论成立
∵△ABC为等边三角形,AD为角平分线,
∴AD垂直平分BC,∠CAD=∠BAD=30°,AB=AC,
∴DB=CD,
∴AC AB =CD DB ;
∵∠C1AB1=60°,
∴∠B1=30°,
∴AB1=2AC1,
又∵∠DAB1=30°,
∴DA=DB1,
而DA=2DC1,
∴DB1=2DC1,
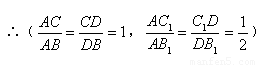
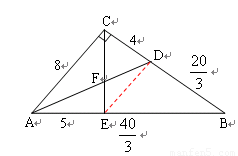
2.结论成立,理由如下:
如图,过点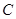 作
作 ∥
∥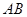 交
交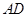 的延长线于点
的延长线于点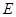 ,则
,则

3.由勾股定理可求

【解析】本题考查了相似三角形的判定与性质:平行于三角形一边的直线被其它两边所截,所截得的三角形与原三角形相似;相似三角形对应边的比相等.也考查了等边三角形的性质、含30°的直角三角形三边的关系以及角平分线的性质

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,点P1,P2,P3,…,P10在反比例函数y=
如图所示,点P1,P2,P3,…,P10在反比例函数y=| 6 |
| x |
A、Q10(
| ||
B、Q10(
| ||
C、Q10(
| ||
| D、Q10(19,0) |
 中,线段
中,线段 为其内角平分线,过
为其内角平分线,过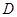 点的直线
点的直线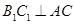 于
于 交
交 的延长线于
的延长线于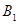 .
.
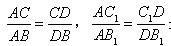 ,是否成立?
,是否成立?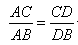 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.