题目内容
如图（1 ）所示：等边△
中，线段
为其内角平分线，过
点的直线
于
交
的延长线于
.
（1）请你探究：
，
是否成立?
（2）请你继续探究：若△
为任意三角形，线段
为其内角平分线，请问
一定成立吗？并证明你的判断.
（3）如图（2）所示
△
中，
，
,
,
为
上一点且
，
交其内角角平分线
与
.试求
的值.
中，线段为其内角平分线，过点的直线于交的延长线于.（1）请你探究：
，是否成立?（2）请你继续探究：若△
为任意三角形，线段为其内角平分线，请问一定成立吗？并证明你的判断.（3）如图（2）所示
△中，，,,为上一点且，交其内角角平分线与.试求的值.
解：（1）结论成立
（
，
）
（2）结论成立，理由如下：如图，过点
作
∥
交
的延长线于点
，
则
，
∴
又∵
平分
∴
∴
∴
∴
（3）由勾股定理可求
由（2）知
即
∴
∴
，
∴
又∵
∴
∴
∴
∥
∴
∴
（
，）（2）结论成立，理由如下：如图，过点
作∥交的延长线于点，则
， ∴
又∵
平分∴
∴
∴
∴（3）由勾股定理可求
由（2）知
即
∴
∴
，∴
又∵
∴
∴
∴
∥∴
∴
练习册系列答案
相关题目
如图，一图形各边长度如图上数据所示，请把该图形分成和它形状相同的四个全等图形．
N，且tan∠MON = 3.
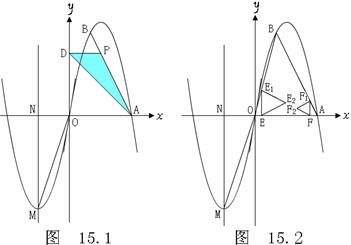②过线段OA上的两点E、F分别作x轴的垂线，交折线 O –B -A于点E1、F1，再分别以线段EE1、FF1为边作如图15.2所示的等边△EE1E2、等边△FF1F2,点E以每秒1个单位长度的速度从点O向点A运动，点F以每秒1个单位长度的速度从点A向点O运动，当△EE1E2有一边与△FF1F2的某一边在同一直线上时，求时间t的值.
