题目内容
18.证明三角形内角和定理三角形内角和定理内容:三角形三个内角和是180°.
已知:
求证:
证明:
分析 先写出已知、证明,过点C作CD∥AB,点E为BC的延长线上一点,利用平行线的性质得到∠1=∠A,∠2=∠B,然后根据平角的定义进行证明.
解答 已 知:△ABC,如图,
知:△ABC,如图,
求证:∠A+∠B+∠ACB=180°,
证明:过点C作CD∥AB,点E为BC的延长线上一点,如图,
∵CD∥AB,
∴∠1=∠A,∠2=∠B,
∵∠ACB+∠1+∠2=180°,
∴∠A+∠B+∠ACB=180°.
点评 本题考查了三角形内角和定理:三角形内角和是180°.本题的关键是把三角形三个角的和转化为一个平角,同时注意文字题证明的步骤书写.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
9.二次函数y=(x-1)2+3的最小值是( )
| A. | 1 | B. | -1 | C. | -3 | D. | 3 |
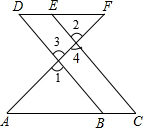 如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.
如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.