题目内容
矩形的两条对角线的一个交角为60°,两条对角线的长度的和为8cm,则这个矩形的一条较长边为________cm.
4
分析:根据矩形的性质推出OA=OB,证出等边△OAB,求出BA,根据勾股定理求出BC即可得到答案.
解答:∵四边形ABCD是矩形,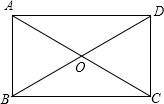
∴AC=BD,OA=OC,OD=OB,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB= AC=4(cm),
AC=4(cm),
∵矩形ABCD,
∴AB=CD=4cm,∠ABC=90°,
在△ABC中,由勾股定理得:BC= =
= =4
=4 (cm),
(cm),
∴AD=BC=4 (cm).
(cm).
故答案是:4 .
.
点评:本题主要考查对矩形的性质,等边三角形的性质和判定,勾股定理等知识点的理解和掌握,能求出AB的长是解此题的关键.

分析:根据矩形的性质推出OA=OB,证出等边△OAB,求出BA,根据勾股定理求出BC即可得到答案.
解答:∵四边形ABCD是矩形,

∴AC=BD,OA=OC,OD=OB,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=
 AC=4(cm),
AC=4(cm),∵矩形ABCD,
∴AB=CD=4cm,∠ABC=90°,
在△ABC中,由勾股定理得:BC=
 =
= =4
=4 (cm),
(cm),∴AD=BC=4
 (cm).
(cm).故答案是:4
 .
.点评:本题主要考查对矩形的性质,等边三角形的性质和判定,勾股定理等知识点的理解和掌握,能求出AB的长是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
矩形的两条对角线的夹角为60°,一条对角线的长为2,则矩形的周长为( )
A、1+
| ||
B、1+2
| ||
C、2+
| ||
D、2+2
|