题目内容
若方程组
的解满足-2≤x+y<0,求m的取值范围.
|
考点:二元一次方程组的解,解一元一次不等式组
专题:
分析:将方程组中两个方程相加,再根据-2≤x+y<0,求得m的取值范围.
解答:解:
,
①+②得,4x+4y=4m+8,
∴x+y=m+2,
∵-2≤x+y<0,
∴
,
由①得,m≥-4,
由②得,m<-2,
∴-4≤m<-2,
故m的取值范围为-4≤m<-2.
|
①+②得,4x+4y=4m+8,
∴x+y=m+2,
∵-2≤x+y<0,
∴
|
由①得,m≥-4,
由②得,m<-2,
∴-4≤m<-2,
故m的取值范围为-4≤m<-2.
点评:本题考查了二元一次方程组和一元一次不等式组的解法,求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).

练习册系列答案
相关题目
一元二次方程kx2+2x-1=0有实数根,则k的范围是( )
| A、k≤-1 |
| B、k>-1且k≠0 |
| C、k<-1 |
| D、k≥-1且k≠0 |
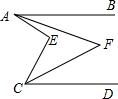 如图,已知AB∥CD,AF平分∠BAE,CF平分∠DCE,若∠BAE=54°,∠DCE=28°,则∠AFC=
如图,已知AB∥CD,AF平分∠BAE,CF平分∠DCE,若∠BAE=54°,∠DCE=28°,则∠AFC= 直线y=2x+8与两坐标轴分别交于P、Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C,若矩形面积为6,试求点A的坐标.
直线y=2x+8与两坐标轴分别交于P、Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C,若矩形面积为6,试求点A的坐标.