题目内容
19. 如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.
如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.(1)求∠AON的度数.
(2)写出∠DON的余角.
分析 (1)根据角平分线的定义求出∠MOB的度数,根据邻补角的性质计算即可.
(2)根据题意得到:∠DOM为∠DON的余角.
解答 解:(1)∵∠AOC+∠AOD=∠AOD+∠BOD=180°,
∴∠BOD=∠AOC=50°,
∵OM平分∠BOD,
∴∠BOM=∠DOM=25°,
又由∠MON=90°,
∴∠AON=180°-(∠MON+∠BOM)=180°-(90°+25°)=65°;
(2)由∠DON+∠DOM=∠MON=90°知∠DOM为∠DON的余角,
故∠DON的余角为:∠DOM.
点评 本题考查的是邻补角的概念以及角平分线的定义,掌握邻补角的性质是邻补角互补是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.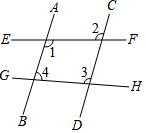 如图,下列判断中正确的是( )
如图,下列判断中正确的是( )
 如图,下列判断中正确的是( )
如图,下列判断中正确的是( )| A. | 如果EF∥GH,那么∠4+∠3=180° | B. | 如果AB∥CD,那么∠1+∠4=180° | ||
| C. | 如果AB∥CD,那么∠1=∠2 | D. | 如果AB∥CD,那么∠2=∠3 |
14.二元一次方程x+2y=10的所有正整数解有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.下列数中,属于无理数的是( )
| A. | $\sqrt{2.5}$ | B. | $\root{3}{-64}$ | C. | 1.5151151115 | D. | $\frac{7π}{2π}$ |
8. 如图,OB⊥OD,OC⊥OA,∠BOC=30°,则∠AOD为( )
如图,OB⊥OD,OC⊥OA,∠BOC=30°,则∠AOD为( )
 如图,OB⊥OD,OC⊥OA,∠BOC=30°,则∠AOD为( )
如图,OB⊥OD,OC⊥OA,∠BOC=30°,则∠AOD为( )| A. | 120° | B. | 130° | C. | 150° | D. | 90° |
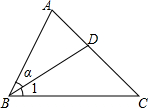 老师提出了以下问题:请用恰当的方法表示图中给出的所有角(小于平角的角),某组同学在本组展示区的答案是:∠1、∠α、∠BAD、∠C、∠D.
老师提出了以下问题:请用恰当的方法表示图中给出的所有角(小于平角的角),某组同学在本组展示区的答案是:∠1、∠α、∠BAD、∠C、∠D. 如图反比例函数y=$\frac{k}{x}$的图象与一次函数y=kx+b的图象交于点A(1,4),点B(-4,n)
如图反比例函数y=$\frac{k}{x}$的图象与一次函数y=kx+b的图象交于点A(1,4),点B(-4,n)