题目内容
7.关于x的方程kx2+(k+3)x+$\frac{k}{4}$=0有两个不相等的实数根.(1)求k的取值范围.
(2)是否存在实数k,使方程的两个实数根的倒数和等于$\frac{28}{5}$?若存在,求出k的值;若不存在,说明理由.
分析 (1)根据一元二次方程的定义和根的判别式得到k≠0且(k+3)2-4k•$\frac{k}{4}$>0,然后求出两个不等式的公共部分即可;
(2)假设存在实数k使方程的两个实数根的倒数和等于$\frac{28}{5}$,利用根与系数的关系得出x1+x2=-$\frac{k+3}{k}$,x1x2=$\frac{1}{4}$,利用两个实数根的倒数和等于$\frac{28}{5}$,得出方程的解,结合k的取值范围判定即可.
解答 解:(1)∵关于x的方程kx2+(k+3)x+$\frac{k}{4}$=0有两个不相等的实数根,
∴k≠0且△>0,即(k+3)2-4k•$\frac{k}{4}$>0,
∴k>-1.5且k≠0.
(2)假设存在实数k使方程的两个实数根的倒数和等于$\frac{28}{5}$,
∵x1+x2=-$\frac{k+3}{k}$,x1x2=$\frac{1}{4}$,
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=-$\frac{4(k+3)}{k}$=$\frac{28}{5}$,
解得:k=-$\frac{5}{4}$,
∴存在实数k使方程的两个实数根的倒数和等于$\frac{28}{5}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
相关题目
18.已知点A(a,2)与点B(3,b)关于x轴对称,则实数a,b的值是( )
| A. | a=3,b=2 | B. | a=-3,b=2 | C. | a=3,b=-2 | D. | a=-3,b=-2 |
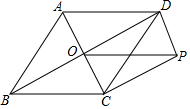 如图,在菱形ABCD中,AC、BD交于点O,BD=8,AC=4,DP∥AC,CP∥BD.
如图,在菱形ABCD中,AC、BD交于点O,BD=8,AC=4,DP∥AC,CP∥BD.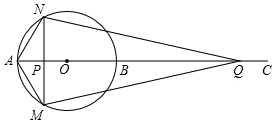 如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为$\frac{3}{2}$cm,AC=8cm,设运动时间为t秒.
如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为$\frac{3}{2}$cm,AC=8cm,设运动时间为t秒. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则抛物线与x轴的另一个交点坐标为(4,0).
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则抛物线与x轴的另一个交点坐标为(4,0).