题目内容
如图，两圆相交于A，B两点，小圆经过大圆的圆心O，点C，D分别在两圆上，若∠ADB=100°，则∠ACB的度数为________．
40°
分析：连接OA，OB，根据圆内接四边形的内对角互补，可得出∠AOB=80°，再根据圆周角定理可求得∠ACB的度数．
解答：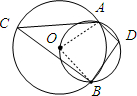
解：如图：连接OA，OB，∵四边形AOBD是圆内接四边形，
∴∠AOB+∠D=180°，
∵∠ADB=100°，
∴∠AOB=80°，
∴∠ACB=40°．
故答案为：40°．
点评：本题考查了圆内接四边形的性质以及圆周角定理，圆内接四边形的内对角互补．
分析：连接OA，OB，根据圆内接四边形的内对角互补，可得出∠AOB=80°，再根据圆周角定理可求得∠ACB的度数．
解答：
解：如图：连接OA，OB，∵四边形AOBD是圆内接四边形，∴∠AOB+∠D=180°，
∵∠ADB=100°，
∴∠AOB=80°，
∴∠ACB=40°．
故答案为：40°．
点评：本题考查了圆内接四边形的性质以及圆周角定理，圆内接四边形的内对角互补．
练习册系列答案
阅读快车系列答案
相关题目
如图，两圆相交于A，B两点，小圆经过大圆的圆心O，点C，D分别在两圆上，若∠ADB=100°，则∠ACB的度数为（ ）| A、35° | B、40° | C、50° | D、80° |
8、如图，两圆相交于C、D，AB是两圆的一条外公切线，A、B为切点，CD的延长线交AB于M，若CD=9，MD=3，则AB的长为（ ）
如图，两圆相交于A，B两点，小圆经过大圆的圆心O，点C、D分别在两圆上，若∠ADB=110°，则∠ACB的度数为（ ）
已知：如图，两圆相交于A，B两点，过A点的割线分别交两圆于D，F点，过B点的割线分别交两圆于H，E点．求证：HD∥EF．
如图，两圆相交于A，B两点，小圆经过大圆的圆心O，点C、D分别在两圆上，若∠ACB=50°，则∠ADB的度数为（ ）