题目内容

通分：
x-y
2x+2y
与
xy
(x+y)2
．
考点：通分
专题：
分析：首先将分母分解因式，进而得出最简公分母求出即可．
解答：解：∵
x-y
2x+2y
=
x-y
2(x+y)
与
xy
(x+y)2
，
∴两式的最简公分母为：2（x+y）2，
∴
x-y
2x+2y
=
x2-y2
2(x+y)2
，
xy
(x+y)2
=
2xy
2(x+y)2
．
点评：此题主要考查了通分，找出最简公分母是解题关键．
练习册系列答案
相关题目
34°20′=
 
°．
在△ABC中，∠BAC＞90°，AB=5，BC=13，AD是BC边上的高，AD=4，求CD和sinC，如果∠BAC＜90°呢？
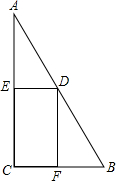如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，点D是AB上的一个动点（不与A、B两点重合），DE⊥AC于点E，DF⊥BC于点F，点D从靠近点A的某一点向点B移动，矩形DECF的周长变化情况是（　　）
A、逐渐减小
B、逐渐增大
C、先增大后减小
D、先减小后增大
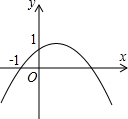如图，二次函数y=ax2+bx+c（a≠0）的图象的顶点在第一象限，且过点（0，1）和（-1，0），下列结论：①ab＜0，②b2＞4a，③0＜a+b+c＜2，④0＜b＜1，⑤当x＞-1时，y＞0．其中正确结论的个数是：
 
．
解方程：
3
x
+
6
x-1
=
x-3
x2-x
．
解方程：
1
11
（2x-3）+
1
19
（3-2x）+
2
13
x=
3
13
．
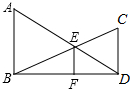已知，如图所示，AB∥CD，AD交BC于点E，EF∥AB交BD于点F．
（1）求证：
1
AB
+
1
CD
=
1
EF
；
（2）若AB=3，CD=4，求EF的长．（提示：原式可化为
EF
AB
+
EF
CD
=1）
如果一个有理数的绝对值是5，那么这个数一定是（　　）
A、5B、-5
C、-5或5D、以上都不对

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网