题目内容
2.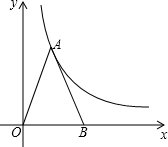 如图,△ABO的面积为3,且AO=AB,反比例函数y=$\frac{k}{x}$的图象经过点A,则k的值为3.
如图,△ABO的面积为3,且AO=AB,反比例函数y=$\frac{k}{x}$的图象经过点A,则k的值为3.
分析 过点A作OB的垂线,垂足为点C,根据等腰三角形的性质得OC=BC,再根据三角形的面积公式得到$\frac{1}{2}$OB•AC=3,易得OC•AC=3,设A点坐标为(x,y),即可得到k=xy=OC•AC=3.
解答 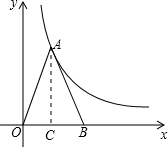 解:过点A作OB的垂线,垂足为点C,如图,
解:过点A作OB的垂线,垂足为点C,如图,
∵AO=AB,
∴OC=BC=$\frac{1}{2}$OB,
∵△ABO的面积为3,
∴$\frac{1}{2}$OB•AC=3,
∴OC•AC=3.
设A点坐标为(x,y),而点A在反比例函数y=$\frac{k}{x}$(k>0)的图象上,
∴k=xy=OC•AC=3.
故答案为:3.
点评 本题考查的是反比例函数比例系数k的几何意义:在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.同时考查了等腰三角形的性质,反比例函数图象上点的坐标特征.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
13.不等式x-4<0的正整数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无数多个 |
7. 如图,直线AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的大小为( )
如图,直线AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的大小为( )
 如图,直线AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的大小为( )
如图,直线AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的大小为( )| A. | 35° | B. | 40° | C. | 50° | D. | 65° |
12.收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻,下面是它们的一些对应的数值:
根据表中波长(m)和频率(kHz)的对应关系,当波长为800m时,频率为375kHz.
| 波长(m) | 300 | 500 | 600 | 1000 | 1500 |
| 频率(kHz) | 1000 | 600 | 500 | 300 | 200 |
