题目内容
6. 如图,已知二次函数y=ax2+bx+8(a≠0)的图象与x轴交于点A(-2,0),
如图,已知二次函数y=ax2+bx+8(a≠0)的图象与x轴交于点A(-2,0),B(4,0)与y轴交于点C.
(Ⅰ)求抛物线的解析式及其顶点D的坐标;
(Ⅱ)求△BCD的面积;
(Ⅲ)若直线CD交x轴与点E,过点B作x轴的垂线,交直线CD与点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究抛物线最多可以向上平移多少个单位长度(直接写出结果,不写求解过程).
分析 (Ⅰ)利用待定系数法求出抛物线的解析式,通过对解析式进行配方能得到顶点D的坐标;
(Ⅱ)先求出直线BC解析式,进而用三角形的面积公式即可得出结论.
(Ⅲ)首先确定直线CD的解析式以及点E,F的坐标,若抛物线向上平移,首先表示出平移后的函数解析式;当x=-8时(与点E横坐标相同),求出新函数的函数值,若抛物线与线段EF有公共点,那么该函数值应不大于点E的纵坐标.当x=4时(与点F的横坐标相同),方法同上,结合上述两种情况,即可得到函数图象的最大平移单位.
解答 解:(Ⅰ)将A、B的坐标代入抛物线的解析式中,得:
$\left\{\begin{array}{l}{4a-2b+8=0}\\{16a+4b+8=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
∴抛物线的解析式:y=-x2+2x+8=-(x-1)2+9,顶点D(1,9);
(Ⅱ)如图1,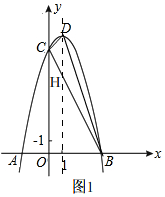
∵抛物线的解析式:y=-x2+2x+8,
∴C(0,8),
∵B(4,0),
∴直线BC解析式为y=-2x+8,
∴直线和抛物线对称轴的交点H(1,6),
∴S△BDC=S△BDH+S△DHC=$\frac{1}{2}$×3×1+$\frac{1}{2}$×3×3=6.
(Ⅲ)如图2,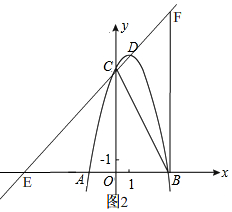
∵C(0,8),D(1,9);
代入直线解析式y=kx+b,
∴$\left\{\begin{array}{l}{b=8}\\{k+b=9}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=8}\end{array}\right.$,
∴y=x+8,
∴E点坐标为:(-8,0),
∵B(4,0),
∴x=4时,y=4+8=12
∴F点坐标为:(4,12),
设抛物线向上平移m个单位长度(m>0),
则抛物线的解析式为:y=-(x-1)2+9+m;
当x=-8时,y=m-72,
当x=4时,y=m,
∴m-72≤0 或 m≤12,
∴0<m≤72,
∴抛物线最多向上平移72个单位.
点评 此题是二次函数综合题,主要考查了函数解析式的确定、函数图象的平移、四边形的内角和、解直角三角形等综合知识.最后一个小题要结合图形来进行解答,若题目没有明确“向上平移”,该题就需要进行分类讨论,要注意解题方法的总结和拓展.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案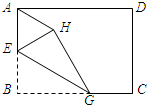 如图,已知长方形纸片ABCD,点E是AB的中点,点G是BC上一点,∠BEG=60°.沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为( )
如图,已知长方形纸片ABCD,点E是AB的中点,点G是BC上一点,∠BEG=60°.沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
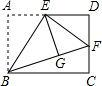 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=$\sqrt{96}$,则DF的长为 ( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=$\sqrt{96}$,则DF的长为 ( )| A. | 2 | B. | 4 | C. | $\sqrt{6}$ | D. | $2\sqrt{3}$ |
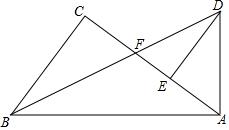 如图,在Rt△ABC和Rt△ABD中,∠C=∠BAD=90°,BD、AC交于点F,且AF=AD,作DE⊥AC于点E.
如图,在Rt△ABC和Rt△ABD中,∠C=∠BAD=90°,BD、AC交于点F,且AF=AD,作DE⊥AC于点E.
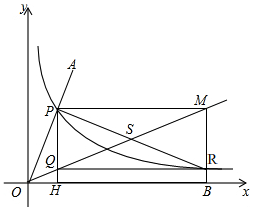 如图,在平面直角坐标系中,射线OA交反比例函数y=$\frac{1}{x}$(x>0)图象于点P,点R为反比例函数y=$\frac{1}{x}$(x>0)图象上的另一点,且PR=2OP,分别过点P、R作x轴、y轴的平行线,两线相交于点M(a,b),直线MR交x轴于点B,过点P作y轴的平行线分别交直线OM和x轴于点Q、H,连接RQ.
如图,在平面直角坐标系中,射线OA交反比例函数y=$\frac{1}{x}$(x>0)图象于点P,点R为反比例函数y=$\frac{1}{x}$(x>0)图象上的另一点,且PR=2OP,分别过点P、R作x轴、y轴的平行线,两线相交于点M(a,b),直线MR交x轴于点B,过点P作y轴的平行线分别交直线OM和x轴于点Q、H,连接RQ.