题目内容
10.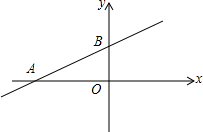 若直线$y=\frac{1}{2}x+2$分别交x轴、y轴于A、B两点,点P是该直线上的一点,PC⊥x轴,C为垂足.
若直线$y=\frac{1}{2}x+2$分别交x轴、y轴于A、B两点,点P是该直线上的一点,PC⊥x轴,C为垂足.(1)求△AOB的面积.
(2)如果四边形PCOB的面积等△AOB的面积的一半,求出此时点P的坐标.
分析 (1)根据直线的解析式求得与坐标轴的交点,然后根据三角形面积公式求得即可;
(2)设P(m,$\frac{1}{2}$m+2),根据梯形的面积公式列出方程解方程即可求得.
解答 解:(1)由y=$\frac{1}{2}$x+2可知A(-4,0),B(0,2),
∴OA=4,OB=2,
∴S△AOB=$\frac{1}{2}$OA•OB=4;
(2)设P(m,$\frac{1}{2}$m+2),
∵四边形PCOB的面积等△AOB的面积的一半,S△AOB=4,
∴四边形PCOB的面积为2,
∴$\frac{1}{2}$(|$\frac{1}{2}$m+2|+2)(|m|)=2,
当m>0时,m2+8m-8=0,求解并舍去负值得m=2$\sqrt{6}-4$;
当0>m≥-4时,m2+8m+8=0,求解并舍去不是这个区间的值,得m=2$\sqrt{2}$-4;
当m<-4时,$\frac{1}{2}{m}^{2}=4$,解得m=$±2\sqrt{2}$(都不合题意,舍去)
解得m=2$\sqrt{6}-4$或m=2$\sqrt{2}$-4,
∴P点坐标为(2$\sqrt{6}-4$,$\sqrt{6}$)或(2$\sqrt{2}$-4,$\sqrt{2}$).
点评 本题考查了一次函数图象上点的坐标特征,三角形面积以及梯形的面积,根据解析式求得与坐标轴的交点是解题的关键.

练习册系列答案
相关题目
17.已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象相交于点A(x1,x2),若x1、x2是关于x的方程x2+mx+2=0的不相等的两实数根,则下列四种说法中错误的是( )
| A. | 必有b≠0 | |
| B. | 必有m2-b2=8 | |
| C. | 线段OA的长度必定大于2 | |
| D. | 除A点外y=$\frac{k}{x}$与y=x+b图象必定还有一个交点,且两交点位于同一象限 |
5.若实数x、y满足$\sqrt{2x-1}+|{y-1}|=0$,则x+y的值是( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
2.若a-b=3,ab=1,则a2+b2的值是( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
19.若$\sqrt{(a-2)^{2}}$=2-a,则a的值( )
| A. | a>2 | B. | a≥2 | C. | a<2 | D. | a≤2 |
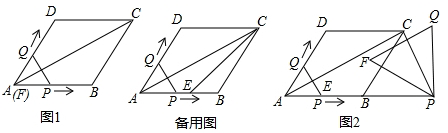
 如图,EF⊥AB,CD⊥AB,∠1=∠3,那么DH∥BC吗?为什么?
如图,EF⊥AB,CD⊥AB,∠1=∠3,那么DH∥BC吗?为什么?