题目内容
有理数a,b,c在数轴上的位置如图所示:

化简下列各式:
(1)|a|-|-b|+|c|;
(2)|a-b|+|b-c|-|c-a|.

化简下列各式:
(1)|a|-|-b|+|c|;
(2)|a-b|+|b-c|-|c-a|.
考点:整式的加减,数轴,绝对值
专题:
分析:根据a、b、c在数轴上的位置可得a<b<0<c,然后进行绝对值的化简,合并即可.
解答:解:由图可得,a<b<0<c,
(1)原式=-a+b+c;
(2)原式=b-a+c-b-c+a
=0.
(1)原式=-a+b+c;
(2)原式=b-a+c-b-c+a
=0.
点评:本题考查了整式的加减,解答本题的关键是根据图示判断出a<b<0<c,并且掌握绝对值的化简.

练习册系列答案
相关题目
某商店出售两件衣服,每件60元,其中一件赚25%,而另一件赔25%,那么这家商店( )
| A、赚了 | B、赔了 |
| C、不赚也不赔 | D、不能确定 |
 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,若CE=12,CF=9,则OC的长是
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,若CE=12,CF=9,则OC的长是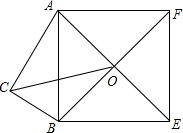 Rt△ABC中,∠C=90°,AC=3,BC=5,以AB为一边向外作正方形ABDF,O为AE、BF交点,则OC长为
Rt△ABC中,∠C=90°,AC=3,BC=5,以AB为一边向外作正方形ABDF,O为AE、BF交点,则OC长为