题目内容
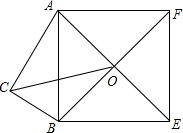 Rt△ABC中,∠C=90°,AC=3,BC=5,以AB为一边向外作正方形ABDF,O为AE、BF交点,则OC长为
Rt△ABC中,∠C=90°,AC=3,BC=5,以AB为一边向外作正方形ABDF,O为AE、BF交点,则OC长为考点:全等三角形的判定与性质,勾股定理,正方形的性质
专题:
分析:延长CA至点D,使AD=BC,再由正方形的性质得出∠AOB=90°,由∠ACB=90°可知∠AOB+∠ACB=180°,由四边形内角和定理可知∠CAO+∠CBO=180°,故可得出∠CBO=∠DAO,由SAS定理可得△COB≌△DOA,故∠COB=∠DOA,OC=OD,由此可得出△COD是等腰直角三角形,根据勾股定理即可得出OC的长.
解答: 解:延长CA至点D,使AD=BC=5,
解:延长CA至点D,使AD=BC=5,
∵四边形ABEF是正方形,
∴∠AOB=90°.
∵∠ACB=90°,
∴∠AOB+∠ACB=180°,
∴∠CAO+∠CBO=180°,
∴∠CBO=∠DAO.
在△COB与△DOA中,
,
∴△COB≌△DOA,
∴∠COB=∠DOA,OC=OD,
∴∠COD=90°,
∴△COD是等腰直角三角形.
∵CD=AC+AD=3+5=8,
∴OC=4
.
故答案为:4
.
 解:延长CA至点D,使AD=BC=5,
解:延长CA至点D,使AD=BC=5,∵四边形ABEF是正方形,
∴∠AOB=90°.
∵∠ACB=90°,
∴∠AOB+∠ACB=180°,
∴∠CAO+∠CBO=180°,
∴∠CBO=∠DAO.
在△COB与△DOA中,
|
∴△COB≌△DOA,
∴∠COB=∠DOA,OC=OD,
∴∠COD=90°,
∴△COD是等腰直角三角形.
∵CD=AC+AD=3+5=8,
∴OC=4
| 2 |
故答案为:4
| 2 |
点评:本题考查的是全等三角形的判定与性质,熟知根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
相关题目
一年之中地球与太阳之间的距离随时间的变化而变化,1个天文单位是地球与太阳之间的平均距离,即1.4960亿km,用科学记数法表示这个数为( )
| A、1.4960×108km |
| B、1.4960×107km |
| C、1.4960×1010km |
| D、1.4960×1011km |
 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD.下列结论:
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD.下列结论:①BC+CE=AB;②BD=
| 1 |
| 2 |
其中不正确的结论有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
在同一时刻,两根长度不等的木杆置于阳光之下,但它们的影长相等,那么这两根木杆可能的相对位置是( )
| A、都垂直于地面 |
| B、都倒在地上 |
| C、平行插在地面 |
| D、斜插在地上 |

 如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF,②△ABE≌△ACD;③BE+DC=DE;④BE2+DC2=DE2,其中正确的是
如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF,②△ABE≌△ACD;③BE+DC=DE;④BE2+DC2=DE2,其中正确的是 如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE.求证:
如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE.求证: 如图,在△ABC中,P为BC上的一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,连接AP,AQ=PQ,PR=PS,给出下面三个结论:①∠BAP=∠CAP;②QP∥AP;③△BRP≌△CSP,其中正确结论的序号是
如图,在△ABC中,P为BC上的一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,连接AP,AQ=PQ,PR=PS,给出下面三个结论:①∠BAP=∠CAP;②QP∥AP;③△BRP≌△CSP,其中正确结论的序号是