题目内容
 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,若CE=12,CF=9,则OC的长是
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,若CE=12,CF=9,则OC的长是考点:勾股定理,等腰三角形的判定与性质,直角三角形斜边上的中线
专题:
分析:根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出EO=FO,再根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF的长,即可得出CO的长.
解答: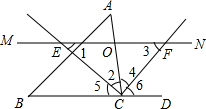 解:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
解:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=12,CF=9,
∴EF=
=15,
∴OC=
EF=7.5.
故答案为:7.5.
 解:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
解:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=12,CF=9,
∴EF=
| 122+92 |
∴OC=
| 1 |
| 2 |
故答案为:7.5.
点评:此题主要考查了勾股定理以及平行线的性质等知识,根据已知得出∠ECF=90°是解题关键.

练习册系列答案
相关题目
单项式-
x2y3的次数是( )
| 2 |
| 3 |
| A、2 | B、3 | C、5 | D、6 |
某小组计划做一批中国结,如果每人做6个,那么比计划多做了9个,如果每人做4个,那么比计划少7个.设计划做x个“中国结”,可列方程( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某商品的价格标签已丢失,售货员只知道“它的进价为80元,打七折售出后,仍可获利4元”,你认为销售员应标在标签上的价格为( )
| A、120元 | B、150元 |
| C、180元 | D、184元 |

 如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF,②△ABE≌△ACD;③BE+DC=DE;④BE2+DC2=DE2,其中正确的是
如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF,②△ABE≌△ACD;③BE+DC=DE;④BE2+DC2=DE2,其中正确的是