题目内容
10.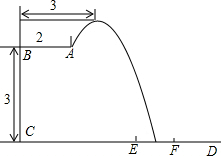 2016年跳水世界杯,于2月19日至24日在巴西里约举行,中国队取得佳绩.优秀成绩的取得离不开艰辛的训练,某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,BC为纵轴建立直角坐标系.
2016年跳水世界杯,于2月19日至24日在巴西里约举行,中国队取得佳绩.优秀成绩的取得离不开艰辛的训练,某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,BC为纵轴建立直角坐标系.(1)当k=4时,求这条抛物线的解析式;
(2)当k=4时,求运动员落水点与点C的距离;
(3)图中CE=$\frac{19}{4}$米,CF=$\frac{21}{4}$米,若跳水运动员在区域EF内(含点E,F)入水时才能达到训练要求,求k的取值范围.
分析 (1)根据抛物线顶点坐标M(3,4),可设抛物线解析为:y=a(x-3)2+4,将点A(2,3)代入可得;
(2)在(1)中函数解析式中令y=0,求出x即可;
(3)若跳水运动员在区域EF内(含点E,F)入水达到训练要求,则在函数y=a(x-3)2+k中当x=$\frac{19}{4}$时y>0,且x=$\frac{21}{4}$时y<0,解不等式即可得.
解答 解:(1)如图所示: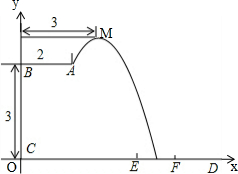
根据题意,可得抛物线顶点坐标M(3,4),A(2,3)
设抛物线解析为:y=a(x-3)2+4,
则3=a(2-3)2+4,
解得:a=-1,
故抛物线解析式为:y=-(x-3)2+4;
(2)由题意可得:当y=0,则0=-(x-3)2+4,
解得:x1=1,x2=5,
故抛物线与x轴交点为:(5,0),
当k=4时,求运动员落水点与点C的距离为5米;
(3)根据题意,抛物线解析式为:y=a(x-3)2+k,
将点A(2,3)代入可得:a+k=3,即a=3-k
若跳水运动员在区域EF内(含点E,F)入水,
则当x=$\frac{19}{4}$时,y=$\frac{49}{16}$a+k≥0,即$\frac{49}{16}$(3-k)+k≥0,
解得:k≤$\frac{49}{11}$,
当x=$\frac{21}{4}$时,y=$\frac{81}{16}$a+k≤0,即$\frac{81}{16}$(3-k)+k≤0,
解得:k≥$\frac{243}{65}$,
故$\frac{243}{65}$≤k≤$\frac{49}{11}$.
点评 此题主要考查了二次函数的应用,根据题意利用顶点式求出二次函数解析式是解题基础,判断入水的位置对应的抛物线上点的坐标特点是解题关键.

练习册系列答案
相关题目
20.y=-x2+(2-a)x+$\frac{9}{4}$是关于x的二次函数,当x的取值范围是1≤x≤5时,y在x=1时取得最大值,则实数a的取值范围是( )
| A. | a≥0 | B. | a≤1 | C. | 0≤a≤1 | D. | a>1 |
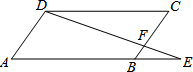 如图,E是?ABCD边AB延长线上的一点,AB=4BE,连接DE交BC于点F,则△DCF与四边形ABFD面积的比是$\frac{2}{3}$.
如图,E是?ABCD边AB延长线上的一点,AB=4BE,连接DE交BC于点F,则△DCF与四边形ABFD面积的比是$\frac{2}{3}$. 如图,在平面直角坐标系中,矩形ABCD的边DA与y轴正半轴重合,D与原点重合.且AD=2,AB=1,以DB为对称轴,将Rt△ADB翻折,点A落在点E处,过E点作EM⊥x轴,垂足是M,另有一点F与点B关于原点对称.
如图,在平面直角坐标系中,矩形ABCD的边DA与y轴正半轴重合,D与原点重合.且AD=2,AB=1,以DB为对称轴,将Rt△ADB翻折,点A落在点E处,过E点作EM⊥x轴,垂足是M,另有一点F与点B关于原点对称. 如图,直线l1∥l2,∠α=∠β,∠1=40°,求∠2的度数.
如图,直线l1∥l2,∠α=∠β,∠1=40°,求∠2的度数.