题目内容
4.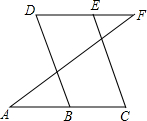 填写理由:如图所示
填写理由:如图所示∵DF∥AC(已知),
∴∠D+∠DBC=180°.(两直线平行,同旁内角互补)
∵∠C=∠D(已知),
∴∠C+∠DBC=180°.(等量代换)
∴DB∥EC.(同旁内角互补,两直线平行)
分析 由平行线的性质,得∠D+∠DBC=180°,利用等量代换得∠C+∠DBC=180,利用平行线的判定定理得出结论.
解答 证明:如图所示,
∵DF∥AC(已知),
∴∠D+∠DBC=180°(两直线平行,同旁内角互补),
∵∠C=∠D(已知),
∴∠C+∠DBC=180°(等量代换),
∴DB∥EC(同旁内角互补,两直线平行 ),
故答案为:两直线平行,同旁内角互补;∠DBC;等量代换;同旁内角互补,两直线平行.
点评 本题主要考查了平行线的性质及判定,利用两直线平行,同旁内角互补和同旁内角互补,两直线平行是解答此题的关键.

练习册系列答案
相关题目
9. 如图,在下列条件中,能判定AB∥CD的是( )
如图,在下列条件中,能判定AB∥CD的是( )
 如图,在下列条件中,能判定AB∥CD的是( )
如图,在下列条件中,能判定AB∥CD的是( )| A. | ∠1=∠3 | B. | ∠2=∠3 | C. | ∠1=∠4 | D. | ∠3=∠4 |
16.将一长方形纸片,如图所示折叠后,再展开.若∠1=50°,则∠2=( )


| A. | 50° | B. | 60° | C. | 65° | D. | 80° |
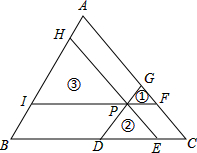 如图,过△ABC内一点分别作三边的平行线,形成三个小三角形①、②、③.已知△ABC的面积的为36,小三角形①、②面积分别为1、4,则小三角形③的面积为9.
如图,过△ABC内一点分别作三边的平行线,形成三个小三角形①、②、③.已知△ABC的面积的为36,小三角形①、②面积分别为1、4,则小三角形③的面积为9.