Question

【题目】五一节前夕，某商店从厂家购进两种礼盒，已知两种礼盒的单价比为，单价和为元

（1）求两种礼盒的单价分别是多少元？

（2）该商店购进这两种礼盒恰好用去元，且购进种礼盒最多个，种礼盒的数量不超过种礼盒数量的倍，共有哪几种进货方案？

（3）根据市场行情，销售一个种礼盒可获利元，销售一个种礼盒可获利元．为奉献爱心，该商店决定每售出一个种礼盒，为爱心公益基金捐款元，每个种礼盒的利润不变，在（2）的条件下，要使礼盒全部售出后所有方案获利相同，的值是多少？此时该商店可获利多少元？

Answer 1

【答案】（1）种礼盒单价为元，种礼盒单价为元；（2）方案有种，第一种: 种礼盒29个，种礼盒个；第二种: 种礼盒32个，种礼盒个；（3），1100元

【解析】

（1）设A种礼盒的单价为2x元，B种礼盒单价为3x元，根据题意列出方程，求出方程的解即可得到结果；

（2）设A种礼盒购进a个，B种礼盒购进b个，根据题意列出不等式组，求出解集确定出所求即可；

（3）设该商店获利W元，表示出W与b的一次函数，根据函数性质确定出所求即可．

解:设种礼盒单价为元，种礼盒单价为元，

依题意得:

解得:

经检验，符合题意.

则.

答:种礼盒单价为元，种礼盒单价为元

设种礼盒购进个，种礼盒购进个，

则

依题意得: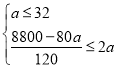

解得:

礼盒个数为整数，

符合的方案有种，分别是:

第一种: 种礼盒29个，种礼盒个；

第二种: 种礼盒32个，种礼盒个；

设该商店获利元，

由可知:

则，

若使所有获利相同相同，则

此时，该商店可获利元．