Question

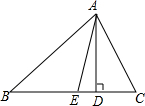（1）如图所示，在△ABC中，AD丄BC于D，AE平分∠BAC，且∠C大于∠B，求证：∠EAD=（∠C-∠B）．
（2）若把问题（1）中的“AD丄BC”改为“点F为EA上一点且FD丄BC于D”，画出新的图形，并试说明∠EFD=（∠C-∠B）．
（3）若把问题（2）中的“F为EA上一点”改为“F为AE延长线上的一点”，则问题（2）中的结论成立吗？请说明你的理由．

Answer 1

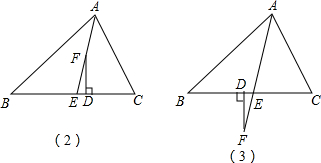（1）证明：在Rt△ADE中，
∵∠AED+∠DAE=90°，
∴∠DAE=90°-∠AED，
∵∠AED=∠AEC=180°-∠C-∠CAE，且AE平分∠BAC，
∴∠CAE=∠BAC=（180°-∠C-∠B），
∴∠DAE=90°-[180°-∠C-（180°-∠C-∠B）]=（∠C-∠B）．

（2）由三角形的外角性质知：∠FED=∠AEC=∠B+∠BAC，
故∠B+∠BAC+∠EFD=90°；①
在△ABC中，由三角形内角和定理得：∠B+∠BAC+∠C=180°，
即：∠C+∠B+∠BAC═90°，②
②-①，得：∠EFD=（∠C-∠B）．

（3）由三角形的外角性质知：∠FED=∠AEC=∠B+∠BAC，
故∠B+∠BAC+∠EFD=90°；①
在△ABC中，由三角形内角和定理得：∠B+∠BAC+∠C=180°，
即：∠C+∠B+∠BAC═90°，②
②-①，得：∠EFD=（∠C-∠B）．
分析：（1）在Rt△ADE中，可得∠AED+∠DAE=90°，又由∠AED=∠AEC=180°-∠C-∠CAE，且AE平分∠BAC，即可证得：∠EAD=（∠C-∠B）．
（2）在△EFD中，由三角形的外角性质知：∠FED=∠AEC=∠B+∠BAC，所以∠B+∠BAC+∠EFD=90°；联立△ABC中，由三角形内角和定理得到的式子，即可推出∠EFD，∠B，∠C的关系．
（3）在△EFD中，由三角形的外角性质知：∠FED=∠AEC=∠B+∠BAC，所以∠B+∠BAC+∠EFD=90°；联立△ABC中，由三角形内角和定理得到的式子，即可推出∠EFD，∠B，∠C的关系．
点评：此题考查了三角形内角和定理、三角形的外角性质以及角平分线的定义．此题难度适中，注意掌握数形结合思想与方程思想的应用．