题目内容
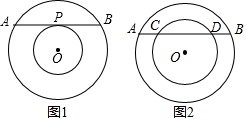
20.圆心相同,半径不相等的两个圆叫做同心圆,用大圆的面积减去小圆的面积就是圆环的面积.(1)如图1,大圆的弦AB切小圆于点P,求证:AP=BP;
(2)若AB=2a,请用含有a的代数式表示图1中的圆环面积;
(3)如图2,若大圆的弦AB交小圆于C、D两点,且AB=8,CD=6,则圆环的面积为7π.
分析 (1)根据切线的性质以及垂径定理即可证明.
(2)根据圆环的面积等于两圆的面积差,再根据切线的性质定理、勾股定理、垂径定理求解.
(3)首先连接OA,OC,由勾股定理可得:OE2=OA2-AE2,OE2=OC2-CE2,继而可得OA2-OC2=7,则可求得圆环的面积
解答 (1)证明:如图1中,连接OP.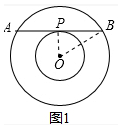
∵AB是小圆的切线,P是切点,
∴OP⊥AB,
∴PA=PB.
(2)解:如图1中,连接OB.
∵大圆的弦AB是小圆的切线,
∴OP⊥AB,AP=PB,
∴OB2-OP2=(2a÷2)2=a2,
∵S圆环=S大-S小=π•OB2-π•OP2=π•(OB2-OP2),
∴S圆环=πa2.
(3)解:如图2中,连接OA,OC,作OE⊥AB于点E.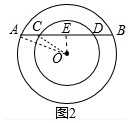
在Rt△AOE与Rt△OCE中:OE2=OA2-AE2,OE2=OC2-CE2,
∴OA2-AE2=OC2-CE2,
∴OA2-OC2=AE2-CE2,
∵AB=8,CD=6,
∴AE=EB=4,CE=DE=3,
∴OA2-OC2=7,
∴圆环的面积为:πOA2-πOC2=π(OA2-OC2)=7π.
故答案为7π.
点评 此题考查了垂径定理、勾股定理、圆的面积的等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,注意数形结合思想的应用,属于中考常考题型.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
13.计算:(-3)+5的结果是( )
| A. | -2 | B. | 2 | C. | 8 | D. | -8 |
12.下列方程中是关于x的一元二次方程的是( )
| A. | x2+$\frac{1}{{x}^{2}}$=1 | B. | (x-1)(x+2)=1 | C. | ax2+bx+c=0 | D. | 3x2-5xy-5y2=0 |
9.金秋十月,又到了食蟹的好季节啦!某经销商去水产批发市场采购太湖蟹,他看中了A、B两家的某种品质相近的太湖蟹.零售价都为60元/千克,批发价各不相同.
A家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
B家的规定如表:
(1)如果他批发80千克太湖蟹,则他在A 家批发需要4416元,在B家批发需要4380元;
(2)如果他批发x千克太湖蟹 (150<x<200),则他在A 家批发需要54x元,在B家批发需要45x+1200元(用含x的代数式表示);
(3)现在他要批发180千克太湖蟹,你能帮助他选择在哪家批发更优惠吗?请说明理由.
A家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
B家的规定如表:
| 数量范围 (千克) | 0~50部分 (含50) | 50以上~150部分(含150,不含50) | 150以上~250部分(含250,不含150) | 250以上部分 (不含250) |
| 价格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(2)如果他批发x千克太湖蟹 (150<x<200),则他在A 家批发需要54x元,在B家批发需要45x+1200元(用含x的代数式表示);
(3)现在他要批发180千克太湖蟹,你能帮助他选择在哪家批发更优惠吗?请说明理由.
10.下列说法中正确的是( )
| A. | 单项式$\frac{3x{y}^{2}}{5}$的系数是3,次数是2 | B. | 单项式-15ab的系数是15,次数是2 | ||
| C. | $\frac{xy-1}{2}$是二次多项式 | D. | 多项式4x2-3的常数项是3 |
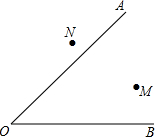 已知∠AOB,点M、N,在∠AOB的内部求作一点P.使点P到∠AOB的两边距离相等,且PM=PN(要求:尺规作图,保留作图痕迹,不写作法).
已知∠AOB,点M、N,在∠AOB的内部求作一点P.使点P到∠AOB的两边距离相等,且PM=PN(要求:尺规作图,保留作图痕迹,不写作法). 已知抛物线的不等式为y=-x2+6x+c.
已知抛物线的不等式为y=-x2+6x+c.