题目内容
8.计算:(1)$\frac{2}{m}-\frac{1}{2m}$=$\frac{3}{2m}$;
(2)$\frac{x-1}{x-2}+\frac{1}{2-x}$=1;
(3)$\frac{bc}{a^2}•\frac{2a}{{{b^2}c}}$=$\frac{2}{ab}$;
(4)$\frac{{2{x^3}}}{y}÷\frac{4x}{{3{y^2}}}$=$\frac{3{x}^{2}y}{2}$.
分析 (1)原式通分并利用同分母分式的减法法则计算即可得到结果;
(2)原式变形后,利用同分母分式的减法法则计算即可得到结果;
(3)原式约分即可得到结果;
(4)原式利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=$\frac{4}{2m}$-$\frac{1}{2m}$=$\frac{3}{2m}$;
(2)原式=$\frac{x-1}{x-2}$-$\frac{1}{x-2}$=$\frac{x-2}{x-2}$=1;
(3)原式=$\frac{2}{ab}$;
(4)原式=$\frac{2{x}^{3}}{y}$•$\frac{3{y}^{2}}{4x}$=$\frac{3{x}^{2}y}{2}$.
故答案为:(1)$\frac{3}{2m}$;(2)1;(3)$\frac{2}{ab}$;(4)$\frac{3{x}^{2}y}{2}$
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13. 如图,下列条件中,能得到DG∥BC的是( )
如图,下列条件中,能得到DG∥BC的是( )
 如图,下列条件中,能得到DG∥BC的是( )
如图,下列条件中,能得到DG∥BC的是( )| A. | CD⊥AB,EF⊥AB | B. | ∠1=∠2 | ||
| C. | ∠1=∠2,∠4+∠5=180° | D. | CD⊥AB,EF⊥AB,∠1=∠2 |
 某人预计步行从家去火车站,从家步行走到6分钟时,以同样的速度回家取忘带的物品,然后从家乘出租赶往火车站,结果到火车站的时间比预计步行的时间提前了3分钟,该人离家的路程s(米)与时间t(分钟)之间的函数图象如图所示,那么从家到火车站的路程是1600m.
某人预计步行从家去火车站,从家步行走到6分钟时,以同样的速度回家取忘带的物品,然后从家乘出租赶往火车站,结果到火车站的时间比预计步行的时间提前了3分钟,该人离家的路程s(米)与时间t(分钟)之间的函数图象如图所示,那么从家到火车站的路程是1600m.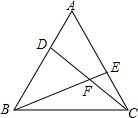 如图,点D、E分别在等边△ABC的AB、AC边上,BE与CD交于F,∠BFC=120°,求证:AD=CE.
如图,点D、E分别在等边△ABC的AB、AC边上,BE与CD交于F,∠BFC=120°,求证:AD=CE.