题目内容
8. 如图,在?ABCD中,点E,F在AC上,且∠ABE=∠CDF,求证:BE=DF.
如图,在?ABCD中,点E,F在AC上,且∠ABE=∠CDF,求证:BE=DF.
分析 根据平行四边形的性质,证明AB=CD,AB∥CD,进而证明∠BAC=∠DCF,根据ASA即可证明△ABE≌△CDF,根据全等三角形的对应边相等即可证明.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
∴△ABE和△CDF中,
$\left\{\begin{array}{l}{∠ABE=∠CDF}\\{AB=CD}\\{∠BAE=∠DCF}\end{array}\right.$,
∴△ABE≌△CDF,
∴BE=DF.
点评 本题考查的是利用平行四边形的性质结合三角形全等来解决有关线段相等的证明.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
18.下列四个几何体中,主视图为圆的是( )
| A. |  | B. |  | C. |  | D. |  |
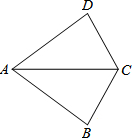 如图,在△ABC与△ADC中,已知AD=AB,在不添加任何辅助线的前提下,要使△ABC≌△ADC,只需再添加的一个条件可以是DC=BC或∠DAC=∠BAC.
如图,在△ABC与△ADC中,已知AD=AB,在不添加任何辅助线的前提下,要使△ABC≌△ADC,只需再添加的一个条件可以是DC=BC或∠DAC=∠BAC. 如图,在?ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,AC⊥BC,则OB=$\sqrt{73}$cm.
如图,在?ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,AC⊥BC,则OB=$\sqrt{73}$cm. 如图所示的几何体是由若干大小相同的小立方块搭成,则这个几何体的左视图是( )
如图所示的几何体是由若干大小相同的小立方块搭成,则这个几何体的左视图是( )



 如图,矩形ABCD中,AB=3,BC=4,则图中五个小矩形的周长之和为14.
如图,矩形ABCD中,AB=3,BC=4,则图中五个小矩形的周长之和为14.