题目内容
8.有四个三角形,分别满足下列条件,其中不是直角三角形的是( )| A. | 一个内角等于另外两个内角之和 | B. | 三个内角之比为3:4:5 | ||
| C. | 三边之比为5:12:13 | D. | 三边长分别为7、24、25 |
分析 根据三角形的内角和定理或勾股定理的逆定理即可进行判断,从而得到答案.
解答 解:A、设两个较小的角为x,则2x+2x=180°,则三角分别为45°,45°,90°,故是直角三角形;
B、设较小的角为3x,则其于两角为4x,5x,则三个角分别为45°,60°,75°,故不是直角三角形;
C、因为52+122=132符合勾股定理的逆定理,故是直角三角形;
D、因为三边符合勾股定理的逆定理,故是直角三角形.
故选B.
点评 本题考查勾股定理的逆定理,判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
18.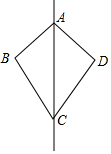 如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )
如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )
 如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )
如图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
20.下列方程为一元二次方程的是( )
| A. | 3x-2=0 | B. | x2-2x-3 | C. | x2-4x-1=0 | D. | xy+1=0 |
17.等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形的一个底角的度数为( )
| A. | 50° | B. | 80° | C. | 50°或80° | D. | 25°或65° |
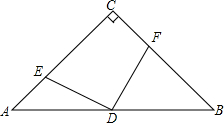 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E在AC上,点F在BC上,且AE=CF.
如图,在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E在AC上,点F在BC上,且AE=CF.