Question

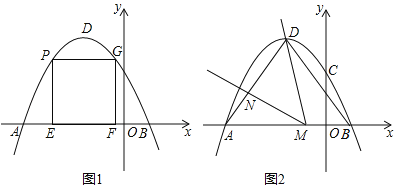
【题目】如图1，二次函数y=-x2+2x+3的图象与x轴交于点A、B，与y轴交于点C，顶点为D．

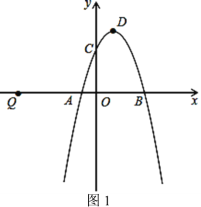
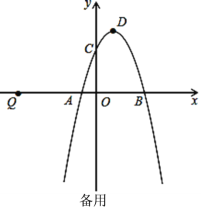
（1）写出A、B、D三点的坐标；

（2）若P（0，t）（t＜-1）是y轴上一点，Q（-5，0），将点Q绕着点P顺时针方向旋转90°得到点E．当点E恰好在该二次函数的图象上时，求t的值；

（3）在（2）的条件下，连接AD、AE．若M是该二次函数图象上一点，且∠DAE=∠MCB，求点M的坐标．

Answer 1

【答案】（1）A（-1，0），B（3，0），D（1，4）；（2）所求t的值为-2；（3）M(，)或M（4，-5）．

【解析】

（1）y=-x2+2x+3，令x=0，则y=3，令y=0，则x=3或-1，即可求解；
（2）△EPH≌△PQO（AAS），则EH=OP=-t，HP=OQ=5，E（-t，5+t），当点E恰好在该二次函数的图象上时，有5+t=-t2-2t+3，即可求解；
（3）分点M在x轴上、点M在x轴两种情况，分别求解即可．

（1）y=-x2+2x+3，令x=0，则y=3，令y=0，则x=3或-1，
故：A（-1，0），B（3，0），D（1，4）；

（2）如图1，过点E作EH⊥y轴于点H，

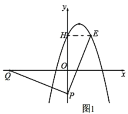
∵∠PQO+∠OPQ=90°，

∠OPQ+∠HPE=90°，

∴∠HPE=∠PQO，

由旋转知，PQ=PE，

∴△EPH≌△PQO(AAS)，

∴EH=OP=-t，

HP=OQ=5

∴E（-t，5+t）

当点E恰好在该二次函数的图象上时，

有5+t=-t2-2t+3

解得t1=-2，t2=-1（由于t＜-1所以舍去），

故所求t的值为-2；

（3）设点M（a，-a2+2a+3）

①若点M在x轴上方，

如图2，过点M作MN⊥y轴于点N，过点D作DF⊥x轴于点F．

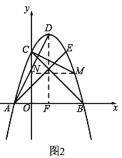
∵∠EAB=∠OCB=45°，

∠DAE=∠MCB

∴∠MCN=∠DAF

∴△MCN∽△DAF，

∴，

∴，a2=0（舍去），

∴M(，) ；

②若点M在x轴下方，

用同样的方法得M（4，-5），

综上所述，M(，)或M（4，-5）．