题目内容
2.一组数99,97,96,98,95的方差是6.分析 先求出这组数据的平均数,再利用方差公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]计算即得.
解答 解:平均数$\overline{x}$=$\frac{1}{5}$(97+98+99+100+101)=99,
方差s2=$\frac{1}{5}$[(99-99)2+(97-99)2+(96-99)2+(98-99)2+(95-99)2]=6,
故答案为:6.
点评 本题主要考查方差的定义,一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
相关题目
12.初二(1)班为元旦文艺表演者发奖,用一定数量的钱去买奖品,若以1支钢笔和2个笔记本为一份奖品,正好能买60份;若以1支钢笔和3本笔记本为一份奖品,正好能买50份;若以1支钢笔和1个笔记本为一份奖品,则这笔钱能买( )份.
| A. | 80 | B. | 70 | C. | 75 | D. | 55 |
13.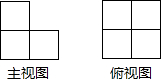 由若干个形状大小相同的小正方体组成的几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数至少有( )
由若干个形状大小相同的小正方体组成的几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数至少有( )
 由若干个形状大小相同的小正方体组成的几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数至少有( )
由若干个形状大小相同的小正方体组成的几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数至少有( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
10.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的体积为( )

| A. | 66 | B. | 36 | C. | 48 | D. | 48$\sqrt{2}$+36 |
17.从分别标有数字-3,-2,-1,0,1,2,3的七张卡片中,随机抽取一张,所抽卡片上数字的绝对值不大于2的概率是( )
| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
7.若函数y=-2x-1与函数y=$\frac{k}{x}$的图象相交于点P(-2,m),则下列各点不在函数y=$\frac{k}{x}$的图象上的是( )
| A. | (3,-2) | B. | (1,-6) | C. | (-1,6) | D. | (-1,-6) |
14.足球比赛规定:胜一场得3分,平一场得1分,负一场得0分,中超联赛某足球队已经进行了7场比赛,得了13分,该队获胜的场数可能是( )
| A. | 2场或3场 | B. | 2场或3场或4场 | C. | 3场或4场 | D. | 3场或4场或5场 |
11.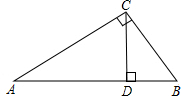 如图,AC⊥BC,CD⊥AB,垂足分别为C、D,下列说法不正确的是( )
如图,AC⊥BC,CD⊥AB,垂足分别为C、D,下列说法不正确的是( )
 如图,AC⊥BC,CD⊥AB,垂足分别为C、D,下列说法不正确的是( )
如图,AC⊥BC,CD⊥AB,垂足分别为C、D,下列说法不正确的是( )| A. | 点A到BC的距离是AC的长度 | B. | 点B到AC的距离是BC的长度 | ||
| C. | 线段BD的长叫D到BC的距离 | D. | 在线段CA、CD、CB中,CD最短 |