题目内容
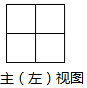
10．一个长方体的三视图如图所示，若其俯视图为正方形，则这个长方体的体积为（ ）
| A． | 66 | B． | 36 | C． | 48 | D． | 48$\sqrt{2}$+36 |
分析 根据对角线为3$\sqrt{2}$，俯视图是一个正方形，则边长为3，再根据长方体体积计算公式即可解答．
解答 解：∵俯视图为正方形，根据主视图可得：正方形的边长为3，长方体的高为4，
∴长方体的体积V=3×3×4=36．
故选：B．
点评 此题考查了由三视图判断几何体，用到的知识点是三视图的基本知识以及长方体体积计算公式．
练习册系列答案
发散思维新课堂系列答案
相关题目
20．甲数是240，乙数比甲数多25%，乙数是（ ）
| A． | 60 | B． | 300 | C． | 260 | D． | 125 |
1．等腰三角形一条边的长为3，它的另两条边的长是关于x的一元二次方程x2-12x+k=0的两个根，则k的值是（ ）
| A． | k=9 | B． | k=27 | C． | k=36 | D． | k=27或k=36 |
18．
由若干个相同的小正方体搭成的几何体的主视图、左视图如图所示，则搭成这个几何体的小正方体的个数最少有（ ）
由若干个相同的小正方体搭成的几何体的主视图、左视图如图所示，则搭成这个几何体的小正方体的个数最少有（ ）| A． | 4个 | B． | 6个 | C． | 8个 | D． | 10个 |
5．
如图，已知直线AB∥CD，∠C=125°，∠E=80°，则∠A的度数为（ ）
如图，已知直线AB∥CD，∠C=125°，∠E=80°，则∠A的度数为（ ）| A． | 45° | B． | 50° | C． | 60° | D． | 70° |
15．-2018的绝对值的倒数是（ ）
| A． | -$\frac{1}{2018}$ | B． | 2018 | C． | $\frac{1}{2018}$ | D． | -2018 |
19．如图（1），PT与⊙O1相切于点T，PAB与⊙O1相交于A、B两点，可证明△PTA∽△PBT，从而有PT2=PA•PB，请应用以上结论解决下列问题：如图（2），PAB、PCD分别与⊙O2相交于A、B、C、D四点，已知PA=2，PB=7，PC=3，则CD=（ ）
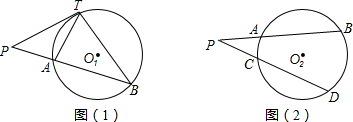
| A． | $\frac{14}{3}$ | B． | $\frac{10}{3}$ | C． | $\frac{5}{3}$ | D． | 4 |