题目内容
19.已知|a-1|-|a-2|的最大值为x,|b+2|+|b-2|的最小值为y,|c-2|+|c+1|+|c|的最小值为z,求:(1)x+2y+3z的值;
(2)a+2b-3c的最小值.
分析 (1)根据绝对值的性质求得x=1,y=4,z=3,再代入计算可得x+2y+3z的值;
(2)根据绝对值的性质求得a,b的最小值分别为:2,-2,c=0,再代入计算可得a+2b-3c的最小值.
解答 解:(1)∵|a-1|-|a-2|的最大值为x,
a-1与a-2是相邻的两个点,
∴|a-1|-|a-2|的最大值为1,
∴x=1,
∵|b+2|+|b-2|的最小值为y,
b+2与b-2是相距4个单位的点,
∴|b+2|+|b-2|的最小值为4,
∴y=4,
∵|c-2|+|c+1|+|c|的最小值为z,
c-2与c+1与c是相距3个单位的3个点,
∴|c-2|+|c+1|+|c|的最小值为3,
∴z=3,
则x+2y+3z的值=1+8+9=18;
(2)由题意得:
当a最小为2时,|a-1|-|a-2|的最大值为1,
当b最小为-2时,|b+2|+|b-2|的最小值为4,
当c=0时,|c-2|+|c+1|+|c|的最小值为3,
则a+2b-3c的最小值=2-4-0=-2.
点评 此题考查了绝对值的最值问题.此题难度适中,解此题的关键是得到x=1,y=4,z=3.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
10.如图1所示,E、F分别为透明正方体的面ADD1A1,面BCC1B1的中心,则四边形BFD1E的正视图、左视图、俯视图分别是图2中的( )
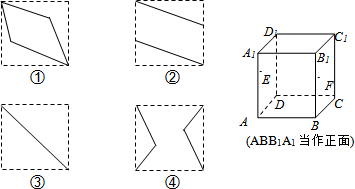

| A. | ②③② | B. | ①②① | C. | ①②③ | D. | ②③④ |
8.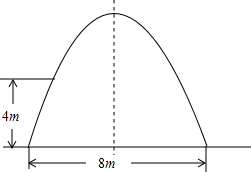 如图,某工厂大门是一抛物线型水泥建筑物,大门地面宽8m,大门高度9m,两侧距地面4m处各有一壁灯,则两壁灯之间水平距离(精确到0.1m,水泥厚度忽略不计)为( )
如图,某工厂大门是一抛物线型水泥建筑物,大门地面宽8m,大门高度9m,两侧距地面4m处各有一壁灯,则两壁灯之间水平距离(精确到0.1m,水泥厚度忽略不计)为( )
 如图,某工厂大门是一抛物线型水泥建筑物,大门地面宽8m,大门高度9m,两侧距地面4m处各有一壁灯,则两壁灯之间水平距离(精确到0.1m,水泥厚度忽略不计)为( )
如图,某工厂大门是一抛物线型水泥建筑物,大门地面宽8m,大门高度9m,两侧距地面4m处各有一壁灯,则两壁灯之间水平距离(精确到0.1m,水泥厚度忽略不计)为( )| A. | 6.0m | B. | 5.3m | C. | 5.6m | D. | 5.9m |
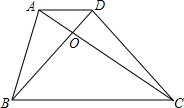 已知:在梯形ABCD中,AD∥BC.
已知:在梯形ABCD中,AD∥BC.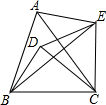 如图,△ABC和△EDC都是等边三角形,连接BD、AE、BE,若∠DBE=15°,则∠AEB的度数为45°.
如图,△ABC和△EDC都是等边三角形,连接BD、AE、BE,若∠DBE=15°,则∠AEB的度数为45°. 如图,填空:
如图,填空: