��Ŀ����
�����������ߵĶ�����ͬ���������Ϊ���Ѻ������ߡ���
������C1��y1=��2x2+4x+2��C2��y2=��x2+mx+nΪ���Ѻ������ߡ���
��1����������C2�Ľ���ʽ��
��2����A��������C2���ڵ�һ���Ķ��㣬��A��AQ��x�ᣬQΪ���㣬��AQ+OQ�����ֵ��
��3����������C2�Ķ���ΪC����B������Ϊ����1��4��������C2�ĶԳ������Ƿ���ڵ�M��ʹ�߶�MB�Ƶ�M��ʱ����ת90��õ��߶�MB�䣬�ҵ�B��ǡ������������C2�ϣ������������M�����꣬������˵�����ɣ�
��ϰ��ϵ�д�
�����Ŀ
5���ⳤΪ1�������������ͼ�ļ����壮

��1���ü����������� ��������λ����������� ��ƽ����λ��
��2�������ü����������ͼ����ͼ
����ͼ ����ͼ
(1)5������λ�������22ƽ�ֵ�λ; (2)��ͼ������. �������������������1�����������������ͱ������ʽ���м��㼴�ɣ� ��2������ͼ��3�У���������ÿһ��С�����ε�����Ϊ2��1��2������ͼ��һ�У�С�����εĸ���Ϊ2�����˻���ͼ�μ��ɣ� �����������1��������������1��1��1��5=5��������λ���� �������1��1��22=22��ƽ����λ���� ��2����ͼ��ʾ��

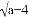 ��0����һԪ���η���kx2��ax��b��0������ʵ��������k��ȡֵ��Χ��________
��0����һԪ���η���kx2��ax��b��0������ʵ��������k��ȡֵ��Χ��________