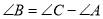题目内容
在平面直角坐标系中,若点P的坐标为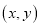 ,则定义:
,则定义: 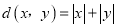 为点P到坐标原点O的“折线距离”.
为点P到坐标原点O的“折线距离”.
(1)若已知P(-2,3),则点P到坐标原点O的“折线距离”d(-2,3)= ;
(2)若点P(x,y)满足2x+y=0,且点P到坐标原点O的“折线距离”d(x,y)=6,求出P的坐标;
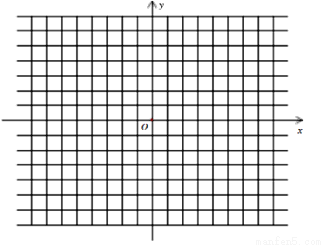
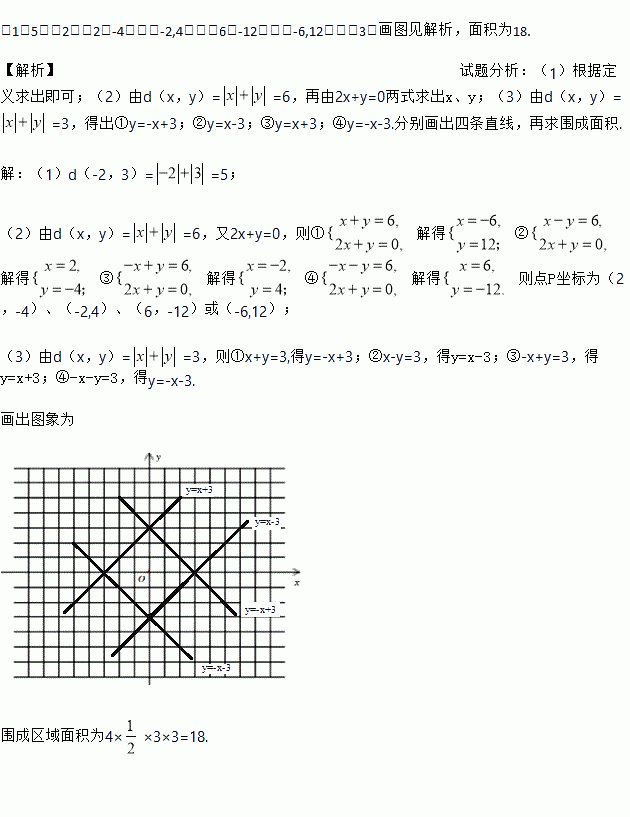
(3)若点P到坐标原点O的“折线距离”d(x,y)=3,试在坐标系内画出所有满足条件的点P构成的图形,并求出该图形的所围成封闭区域的面积.
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

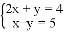
 .
.
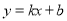 的图象经过点(-2,-4),且与正比例函数
的图象经过点(-2,-4),且与正比例函数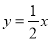 的图象相交于点(4,a),求:
的图象相交于点(4,a),求: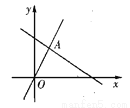
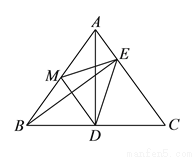
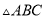 中,
中, 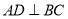 ,垂足为点
,垂足为点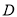 ,
, 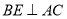 ,垂足为点
,垂足为点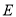 ,
, 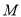 为
为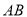 边的中点,连结
边的中点,连结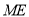 、
、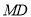 、
、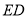 .
.
 )猜想
)猜想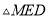 的形状,并说明理由.
的形状,并说明理由.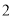 )若
)若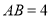 ,
, 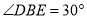 ,求
,求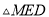 的面积.
的面积.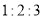 B. 三条边满足关系
B. 三条边满足关系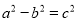
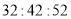 D. 三个角满足关系
D. 三个角满足关系