题目内容
1.在平面直角坐标系中,A(4,0),直线l:y=6与y轴交于点B,点P是直线l上点B右侧的动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=90°,当点P的横坐标满足0≤x≤8,则点Q的运动路径长为8$\sqrt{2}$.分析 如图,作PE⊥OA、作QF⊥BP,证△PEA≌△PFQ,设P(a,6),则PF=PE=6、QF=AE=|4-a|,可得Q(a+6,10-a),即可知点Q始终在直线y=-x+16上运动,由当点P的横坐标满足0≤x≤8时,点Q的横坐标满足6≤x≤14,纵坐标满足2≤y≤10,根据两点间的距离公式求解可得.
解答 解:如图,过点P作PE⊥OA,垂足为E,过点Q作QF⊥BP,垂足为F,
∵BP∥OA,PE⊥OA,
∴∠EPF=∠PEO=90°.
∵∠APQ=90°,
∴∠EPA=∠FPQ=90°-∠APF.
在△PEA和△PFQ中,
∵$\left\{\begin{array}{l}{∠EPA=∠FPQ}\\{∠PEA=∠PFQ=90°}\\{PA=PQ}\end{array}\right.$,
∴△PEA≌△PFQ(AAS),
∴PE=PF,EA=QF,
若点P的坐标为(a,6),则PF=PE=6,QF=AE=|4-a|.
∴点Q的坐标为(a+6,10-a).
∵无论a为何值,点Q的坐标(a+6,10-a)都满足一次函数解析式y=-x+16,
∴点Q始终在直线y=-x+16上运动.
当点P的横坐标满足0≤x≤8时,点Q的横坐标满足6≤x≤14,纵坐标满足2≤y≤10,
则Q的运动路径长为$\sqrt{(6-14)^{2}+(10-2)^{2}}$=8$\sqrt{2}$,
故答案为:8$\sqrt{2}$.
点评 本题主要考查动点的轨迹问题,熟练掌握全等三角形的判定与性质、等腰直角三角形的性质及一次函数的性质、两点间的距离公式是解题的关键.

练习册系列答案
相关题目
11. 如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B的距离,但绳子不够,一位同学帮他想了一个主意:先在地上取一个可以直接达到A的点C,找到AC,BC的中点D,E,并且量得DE的长为15米,则A,B两点间的距离是( )
如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B的距离,但绳子不够,一位同学帮他想了一个主意:先在地上取一个可以直接达到A的点C,找到AC,BC的中点D,E,并且量得DE的长为15米,则A,B两点间的距离是( )
 如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B的距离,但绳子不够,一位同学帮他想了一个主意:先在地上取一个可以直接达到A的点C,找到AC,BC的中点D,E,并且量得DE的长为15米,则A,B两点间的距离是( )
如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B的距离,但绳子不够,一位同学帮他想了一个主意:先在地上取一个可以直接达到A的点C,找到AC,BC的中点D,E,并且量得DE的长为15米,则A,B两点间的距离是( )| A. | 15米 | B. | 20米 | C. | 30米 | D. | 40米 |
6.使二次根式$\sqrt{x-2}$有意义的x的取值范围是( )
| A. | x>2 | B. | x≥2 | C. | x<2 | D. | x>-2 |
13. 如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )
如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )
 如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )
如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
10.-$\frac{1}{3}$的相反数是( )
| A. | -3 | B. | $\frac{1}{3}$ | C. | 3 | D. | -$\frac{1}{3}$ |




 如图,Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,函数y=$\frac{k}{x}$(k>0,x>0)的图象与边AB,OB分别交于点C,D,若S△BCD=1,S△OCD=2,则k的值为$\frac{24}{5}$.
如图,Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,函数y=$\frac{k}{x}$(k>0,x>0)的图象与边AB,OB分别交于点C,D,若S△BCD=1,S△OCD=2,则k的值为$\frac{24}{5}$.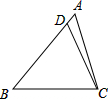 在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2$\sqrt{2}$,AB=3,则AD=$\frac{1}{3}$.
在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2$\sqrt{2}$,AB=3,则AD=$\frac{1}{3}$.