题目内容
在平面直角坐标系内,反比例函数和二次函数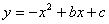 的图象交于点A(m,1)和B(-m,-1)(m≠0).
的图象交于点A(m,1)和B(-m,-1)(m≠0).
(1)当m=2时,分别求反比例函数和二次函数的解析式;
(2)若二次函数的顶点在反比例函数上,求出此时的m值;
(3)当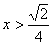 时,这两个函数的增减性一致,请写出满足条件的最小整数m.
时,这两个函数的增减性一致,请写出满足条件的最小整数m.
(1)当m=2时,A(2,1)和B(-2,-1),
∴反比例函数解析式为
把A(2,1)和B(-2,-1)代入 得b=
得b= ,c=4,
,c=4,
∴二次函数的解析式为
(2)∵反比例函数和二次函数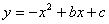 的图象交于点A(m,1)和B(-m,-1)
的图象交于点A(m,1)和B(-m,-1)
∴
∴
∴二次函数的顶点为
又∵二次函数的顶点在反比例函数上
∴
∴
(3)∵二次函数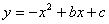 的图象的开口方向向下
的图象的开口方向向下
∴当 时,y随x的增大而减小
时,y随x的增大而减小
又∵当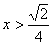 时,这两个函数的增减性一致
时,这两个函数的增减性一致
∴
∴
∴m的最小整数为2.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
|
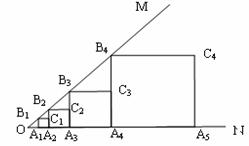
 中,A、B两点的坐标分别为A(2,4),B(a,-4)(其中a>0),∠AOB=90°,点C在
中,A、B两点的坐标分别为A(2,4),B(a,-4)(其中a>0),∠AOB=90°,点C在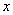 轴的正半轴上.动点P从点O出发,在四边形OACB的边上依次沿O→A→C→B向点B移动,当点P与点B重合时停止运动.设点P移动的路径的长为
轴的正半轴上.动点P从点O出发,在四边形OACB的边上依次沿O→A→C→B向点B移动,当点P与点B重合时停止运动.设点P移动的路径的长为 ,△POB的面积为
,△POB的面积为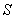 ,
,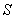 与
与 的函数关系的图象如图2所示,其中四边形ODEF是梯形.
的函数关系的图象如图2所示,其中四边形ODEF是梯形. (1)结合以上信息及图2填空:图2中的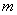 = ;
= ;
(2)求B,C两点的坐标及图2中OF的长;
(3)在图1中,当动点P恰为经过O、C两点的抛物线的顶点时,
①求此抛物线的解析式;
②若点Q在抛物线上,满足以C、P、Q三点为顶点的三角形是直角三角形,求点Q的坐标.


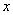 的一元二次方程
的一元二次方程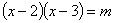 有实数根
有实数根 ,且
,且 ,有下列结论:
,有下列结论: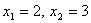 ;②
;②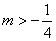 ;③当
;③当 时,
时, ;④二次函数
;④二次函数 图象与
图象与 ,若m是不等式组
,若m是不等式组 的整数解,求此分式的值。
的整数解,求此分式的值。