题目内容
|
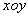 中,A、B两点的坐标分别为A(2,4),B(a,-4)(其中a>0),∠AOB=90°,点C在
中,A、B两点的坐标分别为A(2,4),B(a,-4)(其中a>0),∠AOB=90°,点C在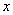 轴的正半轴上.动点P从点O出发,在四边形OACB的边上依次沿O→A→C→B向点B移动,当点P与点B重合时停止运动.设点P移动的路径的长为
轴的正半轴上.动点P从点O出发,在四边形OACB的边上依次沿O→A→C→B向点B移动,当点P与点B重合时停止运动.设点P移动的路径的长为 ,△POB的面积为
,△POB的面积为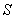 ,
,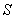 与
与 的函数关系的图象如图2所示,其中四边形ODEF是梯形.
的函数关系的图象如图2所示,其中四边形ODEF是梯形. (1)结合以上信息及图2填空:图2中的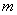 = ;
= ;
(2)求B,C两点的坐标及图2中OF的长;
(3)在图1中,当动点P恰为经过O、C两点的抛物线的顶点时,
①求此抛物线的解析式;
②若点Q在抛物线上,满足以C、P、Q三点为顶点的三角形是直角三角形,求点Q的坐标.

解:(1) 
(2)①B(8,-4)
②C10,0) 
(3)∵抛物线过(0,0)(10,0) P(5, )
)
∴
可证四边形OACB为矩形
显然∠Q=90°
∴①当∠PCB=90°时,
可由B(8,-4),C(10,0)得
直线BC:y=-2x-20,与 的交点Q(-20,-60)
的交点Q(-20,-60)
同理②当∠CPQ=90°时 Q(-15, )
)


练习册系列答案
相关题目
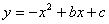 的图象交于点A(m,1)和B(-m,-1)(m≠0).
的图象交于点A(m,1)和B(-m,-1)(m≠0). 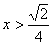 时,这两个函数的增减性一致,请写出满足条件的最小整数m.
时,这两个函数的增减性一致,请写出满足条件的最小整数m. )。
)。
 的无理数:____ ___.
的无理数:____ ___.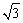 ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.(结果精确到0.1米,参考数据:
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.(结果精确到0.1米,参考数据:
 且AB>BC,那么下列最确切的结论是( ).
且AB>BC,那么下列最确切的结论是( ). D、AC=BC
D、AC=BC B、-0.2 C、
B、-0.2 C、