题目内容
4.已知点A在数轴表示的数是2a-1,点B在数轴上表示的数是3a-2,若线段AB的中点恰为原点O,则a=$\frac{3}{5}$,B点表示的数是-$\frac{1}{5}$.分析 根据点A在数轴表示的数是2a-1,点B在数轴上表示的数是3a-2,线段AB的中点恰为原点O,可知$\frac{(2a-1)+(3a-2)}{2}=0$,从而可以求得a的值,点B表示的数,从而本题得以解决.
解答 解:∵点A在数轴表示的数是2a-1,点B在数轴上表示的数是3a-2,若线段AB的中点恰为原点O,
∴$\frac{(2a-1)+(3a-2)}{2}=0$,
解得,a=$\frac{3}{5}$,
∴3a-2=3×$\frac{3}{5}$-2=$-\frac{1}{5}$,
即点B表示的数是$-\frac{1}{5}$,
故答案为:$\frac{3}{5},-\frac{1}{5}$.
点评 本题考查数轴,解题的关键是明确线段中点的意义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知x=-5是方程2k-x=7的解,则k的值是( )
| A. | 1 | B. | -1 | C. | 6 | D. | -6 |
19.若M=2a2b,N=7ab2,P=-4a2b,则下列等式成立的是( )
| A. | M+N=9a2b | B. | N+P=3ab | C. | M+P=-2a2b | D. | M-P=2a2b |
13.有一个袋子里装有6个红球,5个白球,1个黑球,每个球除了颜色外,其他都相同,任意摸出一个球,则最有可能摸到的是( )
| A. | 红球 | B. | 白球 | C. | 黑球 | D. | 无法确定 |
 如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米,
如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米,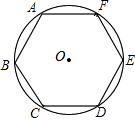 如图,正六边形ABCDEF内接于⊙O,向⊙O内任意投点,则所投的点落在正六边形ABCDEF内的概率是$\frac{3\sqrt{3}}{2π}$.
如图,正六边形ABCDEF内接于⊙O,向⊙O内任意投点,则所投的点落在正六边形ABCDEF内的概率是$\frac{3\sqrt{3}}{2π}$.