题目内容

5．如图，将△ABC沿直线AD翻折，使点B与AC边上的点E重合，若AB=AD=5，AC=9，则DC=6．

分析 先设∠B=x，先由平角的性质及三角形可得到∠EDC=∠BAD，再利用图形翻折变换的性质可得到∠BAD=∠DAE，由相似三角形的判定定理可得到△DCE∽△ACD，根据相似三角形的对应边成比例即可解答．

解答 解：设∠B=x，
在△ABE中，∠BAE=180°-2x，
∵∠EDC=180°-∠ADB-∠ADE=180°-2x，
∴∠BAD=∠EDC，
∵∠BAD=∠DAE，∠C=∠C，
∴∠DAE=∠EDC，
∴△DCE∽△ACD，
∴$\frac{EC}{DC}$=$\frac{DC}{AC}$=$\frac{9-5}{DC}$=$\frac{DC}{9}$，
所以DC=$\sqrt{（9-5）×9}$=6．
故答案为：6．

点评 本题考查的是图形的翻折变换、等腰三角形的性质、三角形内角和定理、相似三角形的判定与性质，涉及面较广，难易适中．

练习册系列答案
相关题目
6．八（3）班为了组队参加学校举行的“五水共治”知识竞赛，在班里选取了若干名学生，分成人数相同的甲、乙两组，对两组学生进行四次“五水共治”模拟竞赛，成绩优秀的人数和优秀率分别绘制成如下统计图．

根据统计图，解答下列问题：
（1）请计算第三次模拟竞赛成绩的优秀率是多少？并将条形统计图与折线统计图补充完整；
（2）已求得甲组四次成绩优秀的平均人数为7，甲组四次成绩优秀人数的方差为1.5，请通过计算乙组的相关数据，判断哪一组成绩优秀的人数较稳定？
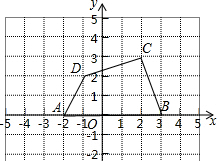7．如图，四边形ABCD的各顶点的坐标分别为A（-2，0），B（3，0），C（2，4），D（-1，2）．
（1）将各顶点的纵坐标不变，横坐标各增加3，得到点A1、B1、C1、D1，写出A1、B1、C1、D1各点的坐标；
（2）若将点A1、B1、C1、D1依次连接起来，得到四边形A1B1C1D1，则四边形A1B1C1D1与原四边形ABCD相比有什么变化？
（3）若横坐标不变，纵坐标各增加3，得到的四边形A2B2C2D2与四边形ABCD相比有什么变化？
13．在正常情况下，一个人在运动时所能承受的每分钟心跳的最高次数S（次/分）与这个人年龄n（岁）满足关系式：S=an+b，其中a、b均为常数．
（1）根据图中提供的信息，求a、b的值；
（2）若一位63岁的人在跑步，医生在途中给他测得10秒心跳为26次，问：他是否有危险？为什么？
20．如图，直线MN交⊙O于点A、B，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于点E．
（1）DE与⊙O有何位置关系？说明理由；
（2）若DE=4cm，AE=2cm，求⊙O的半径．
10．如图，点O、A、B在同一直线上，OC平分∠AOD，OE平分∠FOB，∠COF=∠DOE=90°．
（1）∠COD与∠EOF有什么数量关系？说明理由．
答：∠COD=∠EOF，
理由如下：∵∠COF=∠DOE，
∴∠COF-∠DOF=∠DOE-∠DOF．
∴结论成立．
（2）∠AOC与∠BOF有什么数量关系？说明理由．
理由如下：∵OC平分∠AOD，OE平分∠FOB，
∴∠COD=∠AOC，∠BOF=2∠EOF，
∵由（1）得到的∠COD与∠EOF关系．
∴∠AOC与∠BOF的数量关系为2∠AOC=∠BOF．
（3）求∠AOD的度数．
17．抛物线y=-2x2+4x+5的对称轴为（　　）
A．x=1B．x=-1C．x=2D．x=-2
14．尺规作图．
如图，已知在平面上有三个点A，B，C，请按下列要求作图：
（1）作直线AB；
（2）作射线AC；
（3）在射线AC上作线段AD，使AD=2AB．
15．中国是世界上13个贫水国家之一．某校有800名在校学生，学校为鼓励学生节约用水，展开“珍惜水资源，节约每一滴水”系列教育活动．为响应学校号召，数学小组做了如下调查：
小亮为了解一个拧不紧的水龙头的滴水情况，记录了滴水时间和烧杯中的水面高度，
如图1．小明设计了调查问卷，在学校随机抽取一部分学生进行了问卷调查，并制作出统计图．如图2和图3．

请结合图2和图3回答下列问题：
（1）参加问卷调查的学生人数为60人，其中选C的人数占调查人数的百分比为10%．
（2）在这所学校中选“比较注意，偶尔水龙头滴水”的大概有440人．若在该校随机抽取一名学生，这名学生选B的概率为0.55．
请结合图1解答下列问题
（3）在“水龙头滴水情况”图中，水龙头滴水量（毫升）与时间（分）可以用我们学过的哪种函数表示？请求出函数关系式．
（4）为了维持生命，每人每天需要约2400毫升水，该校选C的学生因没有拧紧水龙头，2小时浪费的水可维持多少人一天的生命需要？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网