题目内容
7.已知x2-4=0,求代数式$\frac{(x-1)^{2}}{{x}^{2}-1}$+$\frac{{x}^{2}}{x+1}$的值.分析 先把分母因式分解,约分后进行同分母的加法运算得到原式=$\frac{{x}^{2}+x-1}{x+1}$,再由x2-4=0解得x=2或x=-2,然后把x=2或x=-2分别代入原式计算相应的代数式的值.
解答 解:原式=$\frac{(x-1)^{2}}{(x+1)(x-1)}$+$\frac{{x}^{2}}{x+1}$
=$\frac{x-1}{x+1}$+$\frac{{x}^{2}}{x+1}$
=$\frac{{x}^{2}+x-1}{x+1}$,
∵x2-4=0,
∴x=2或x=-2,
当x=2时,原式=$\frac{4+2-1}{2+1}$=$\frac{5}{3}$;
当x=-2时,原式=$\frac{4-2-1}{-2+1}$=-1.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
16.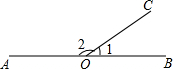 如图,若∠AOB=180°,∠1是锐角,则∠1的余角是( )
如图,若∠AOB=180°,∠1是锐角,则∠1的余角是( )
 如图,若∠AOB=180°,∠1是锐角,则∠1的余角是( )
如图,若∠AOB=180°,∠1是锐角,则∠1的余角是( )| A. | $\frac{1}{2}$∠2-∠1 | B. | $\frac{1}{2}$(∠2-∠1) | C. | $\frac{1}{2}$∠2-$\frac{3}{2}$∠1 | D. | $\frac{1}{3}$(∠2+∠1) |