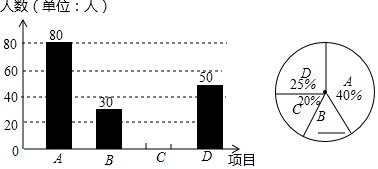
题目内容
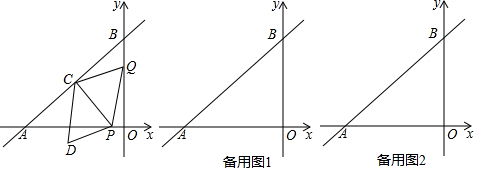
2. 在平面直角坐标xOy中,直线y=kx+1(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)的一个交点为A(-2,3),与x轴交于点B.
在平面直角坐标xOy中,直线y=kx+1(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)的一个交点为A(-2,3),与x轴交于点B.(1)求m的值和点B的坐标;
(2)点P在y轴上,点P到直线y=kx+1(k≠0)的距离为$\sqrt{2}$,直接写出点P的坐标.
分析 (1)把A(-2,3)分别代入y=kx+1(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)即可得到结论;
(2)设P(0,n),根据已知条件列方程即可得到结论.
解答 解:(1)∵双曲线y=$\frac{m}{x}$(m≠0)经过点,A(-2,3),
∴m=-6,
∵直线y=kx+1(k≠0)经过点A(-2,3),
∴k=-1,
∴y=-x+1,
令y=0,则-x+1=0,
∴x=1,
∴B(1,0);
(2)∵点P在y轴上,
∴设P(0,n),
∵点P到直线y=-x+1(k≠0)的距离为$\sqrt{2}$,
∴$\frac{|n-1|}{\sqrt{{1}^{2}+{1}^{2}}}$=$\sqrt{2}$,
∴n=3,n=-1,
∴P(0,3)或(0,-1).
点评 本题考查了一次函数与反比例函数的交点问题,点到直线的距离公式,熟练掌握点到直线的距离公式是解题的关键.

练习册系列答案
相关题目
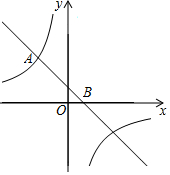
10. 把一个边长为1的正方形如图所示放在数轴上,以正方形的对角线为半径画弧交数轴于点A,则点A对应的数是( )
把一个边长为1的正方形如图所示放在数轴上,以正方形的对角线为半径画弧交数轴于点A,则点A对应的数是( )
 把一个边长为1的正方形如图所示放在数轴上,以正方形的对角线为半径画弧交数轴于点A,则点A对应的数是( )
把一个边长为1的正方形如图所示放在数轴上,以正方形的对角线为半径画弧交数轴于点A,则点A对应的数是( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
7.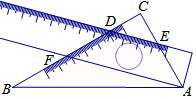 一个三角板(含30°、60°角)和一把直尺摆放位置如图所示,直尺与三角板的一角相 交于点A,一边与三角板的两条直角边分别相交于点D、点E,且CD=CE,点F在直尺的另一边上,那么∠BAF的大小为( )
一个三角板(含30°、60°角)和一把直尺摆放位置如图所示,直尺与三角板的一角相 交于点A,一边与三角板的两条直角边分别相交于点D、点E,且CD=CE,点F在直尺的另一边上,那么∠BAF的大小为( )
 一个三角板(含30°、60°角)和一把直尺摆放位置如图所示,直尺与三角板的一角相 交于点A,一边与三角板的两条直角边分别相交于点D、点E,且CD=CE,点F在直尺的另一边上,那么∠BAF的大小为( )
一个三角板(含30°、60°角)和一把直尺摆放位置如图所示,直尺与三角板的一角相 交于点A,一边与三角板的两条直角边分别相交于点D、点E,且CD=CE,点F在直尺的另一边上,那么∠BAF的大小为( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
14.计算|-4+1|的结果是( )
| A. | -5 | B. | -3 | C. | 3 | D. | 5 |