题目内容
8. 如图,AB为⊙O的直径,点C、F在⊙O上,ED⊥AF于D,AF、BC交于M,∠E=2∠ABC,
如图,AB为⊙O的直径,点C、F在⊙O上,ED⊥AF于D,AF、BC交于M,∠E=2∠ABC,(1)求证:AC=CF;
(2)若DE=1,AE=$\sqrt{10}$,求$\frac{AC}{BM}$的值.
分析 (1)要证明AC=CF,只要证明∠ABC=∠CBF即可,根据题目中的条件,利用平行线的性质和圆周角定理可以证明∠ABC=∠CBF,本题得以解决;
(2)要求$\frac{AC}{BM}$的值,只需要证明△ACN∽△BFM即可,根据题意目中的条件可以找出这两个三角形相似,从而可以解答本题.
解答 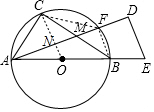 (1)证明:连接BF,CF,如右图所示,
(1)证明:连接BF,CF,如右图所示,
∵AB是⊙O的直径,
∴∠AFB=90°,
∵ED⊥AF,
∴∠ADE=90°,
∴∠AFB=∠ADE,
∴BF∥ED,
∴∠AED=∠ABF,
∵∠E=2∠ABC,
∴∠ABF=2∠ABC,
∵∠ABC=∠CBF,
∴AC=CF;
(2)由(1)知AC=CF,
连接OC交AF于点N,则OC⊥AF,
∴∠ANC=90°,
∵∠CAN=∠FBM,∠ANC=∠BFM=90°,
∴△ACN∽△BFM,
∴$\frac{AC}{BM}=\frac{AN}{BF}$,
∵DE=1,AE=$\sqrt{10}$,BF∥ED,
∴△ABF∽△AED,
∴$\frac{AB}{BF}=\frac{AE}{ED}$=$\frac{\sqrt{10}}{1}$,
设BF=a,则AB=$\sqrt{10}$a,AF=3a,
∴$\frac{AC}{BM}=\frac{AN}{BF}$=$\frac{\frac{3a}{2}}{a}=\frac{3}{2}$,
点评 本题考查相似三角形的判定与性质、圆周角定理,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用三角形相似和圆周角定理解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.王老师将八年级一班、二班学生的数学期中成绩(满分100分)统计如下:
小明由此得到如下结论,其中不一定正确的是( )
| 班级 | 考试人数 | 平均分 | 中位数 | 众数 | 方差 |
| 一班 | 51 | 80 | 84 | 88.78 | 186 |
| 二班 | 51 | 80 | 86 | 78 | 161 |
| A. | 一班、二班学生成绩的平均数相同 | |
| B. | 二班优生多于一班(优生为85分或85分以上者) | |
| C. | 二班成绩比一班整齐 | |
| D. | 成绩为78分的学生二班比一班多 |
 我市某居民区一处圆形地下水管道破裂,修理工人准备更换一段新管道,经测量得到如图所示的数据,水面宽度AB=60厘米,水面到管顶的距离为10厘米,那么修理工人应准备直径为100厘米的管道.
我市某居民区一处圆形地下水管道破裂,修理工人准备更换一段新管道,经测量得到如图所示的数据,水面宽度AB=60厘米,水面到管顶的距离为10厘米,那么修理工人应准备直径为100厘米的管道. 把一副三角板按如图叠放在一起,则∠1=75度.
把一副三角板按如图叠放在一起,则∠1=75度.