题目内容
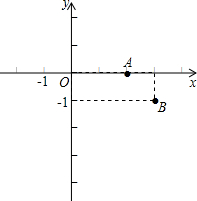 如图,在平面直角坐标系xOy中,点A、B的坐标分别为(2,0)、(3,-1),二次函数y=-x2的图象为C1.
如图,在平面直角坐标系xOy中,点A、B的坐标分别为(2,0)、(3,-1),二次函数y=-x2的图象为C1.(1)向上平移抛物线C1,使平移后的抛物线C2经过点A,求抛物线C2的表达式;
(2)平移抛物线C1,使平移后的抛物线C3经过点A、B两点,抛物线C3与y轴交于点D,求抛物线C3的表达式以及点D的坐标;
(3)在(2)的条件下,记OD中点为E,点P为抛物线C3对称轴上一点,当△ABP与△ADE相似时,求点P的坐标.
考点:二次函数综合题,相似三角形的判定与性质
专题:综合题,分类讨论
分析:(1)根据条件可设抛物线C2的解析式为y=-x2+c,然后把点A的坐标代入y=-x2+c,就可解决问题;
(2)根据条件可设抛物线C3的解析式为y=-x2+mx+n,然后把点A、B的坐标代入y=-x2+mx+n,就可求出抛物线C3的解析式,然后令x=0就可求出点D的坐标;
(3)过点B作BH⊥x轴于点H,可求得∠HAB=45°,AB=
.结合条件易求得∠DEA=135°,
=
.若点P在点A的下方,则∠BAP=45°,由△ABP与△ADE相似可得∠ABP或∠APB为135°,与三角形内角和矛盾,该情况不存在,因而点P必在点A的上方.然后只需分两种情况讨论,运用相似三角形的性质可求出点P的坐标.
(2)根据条件可设抛物线C3的解析式为y=-x2+mx+n,然后把点A、B的坐标代入y=-x2+mx+n,就可求出抛物线C3的解析式,然后令x=0就可求出点D的坐标;
(3)过点B作BH⊥x轴于点H,可求得∠HAB=45°,AB=
| 2 |
| DE |
| AE |
| 1 | ||
|
解答:解:(1)设抛物线C2的解析式为y=-x2+c,
∵抛物线C2经过点A(2,0),
∴-4+c=0,
∴c=4,
∴抛物线C2的解析式为y=-x2+4;
(2)设抛物线C3的解析式为y=-x2+mx+n,
∵抛物线C3经过点A(2,0)、B(3,-1),
∴
,
解得:
,
∴抛物线C3的解析式为y=-x2+4x-4.
当x=0时,y=-4,故点D的坐标为(0,-4);
(3)过点B作BH⊥x轴于点H,则有AH=BH=1,
∴∠HAB=∠HBA=45°,AB=
.
∵D的坐标为(0,-4),
∴OD=4.
∵点E为OD中点,
∴OE=DE=2.
在Rt△AOE中,
∵∠AOE=90°,OA=OE=2,
∴AE=2
,∠OEA=∠OAE=45°,
∴∠DEA=135°,
=
=
.
若点P在点A的下方,则∠BAP=45°,
由△ABP与△ADE相似可得∠ABP或∠APB为135°,
与三角形内角和矛盾,该情况不存在.
∴点P必在点A的上方.
①若△ABP∽△EAD,如图1,

则
=
=
,
∴AP=
×
=1,
∴点P的坐标为(2,1);
②若△ABP∽△EDA,如图2,

则
=
=
,
∴AP=
AB=
×
=2,
∴点P的坐标为(2,2).
∵抛物线C2经过点A(2,0),
∴-4+c=0,
∴c=4,
∴抛物线C2的解析式为y=-x2+4;
(2)设抛物线C3的解析式为y=-x2+mx+n,
∵抛物线C3经过点A(2,0)、B(3,-1),
∴
|
解得:
|
∴抛物线C3的解析式为y=-x2+4x-4.
当x=0时,y=-4,故点D的坐标为(0,-4);
(3)过点B作BH⊥x轴于点H,则有AH=BH=1,
∴∠HAB=∠HBA=45°,AB=
| 2 |
∵D的坐标为(0,-4),
∴OD=4.
∵点E为OD中点,
∴OE=DE=2.
在Rt△AOE中,
∵∠AOE=90°,OA=OE=2,
∴AE=2
| 2 |
∴∠DEA=135°,
| DE |
| AE |
| 2 | ||
2
|
| 1 | ||
|
若点P在点A的下方,则∠BAP=45°,
由△ABP与△ADE相似可得∠ABP或∠APB为135°,
与三角形内角和矛盾,该情况不存在.
∴点P必在点A的上方.
①若△ABP∽△EAD,如图1,

则
| AP |
| AB |
| ED |
| EA |
| 1 | ||
|
∴AP=
| 1 | ||
|
| 2 |
∴点P的坐标为(2,1);
②若△ABP∽△EDA,如图2,

则
| AB |
| AP |
| ED |
| EA |
| 1 | ||
|
∴AP=
| 2 |
| 2 |
| 2 |
∴点P的坐标为(2,2).
点评:本题主要考查了用待定系数法求抛物线的解析式、等腰三角形的性质、勾股定理、相似三角形的判定与性质等知识,运用反证法及分类讨论的思想是解决第(3)小题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若关于x的一元二次方程ax2+bx-1=0(a≠0)有一个根为-1,则2016-a+b的值是( )
| A、2017 | B、2015 |
| C、2014 | D、2013 |
 如图,M,N是线段AB上的两点,且N是线段AM的中点,若AB=14cm,BM=6cm,则AN的长为( )
如图,M,N是线段AB上的两点,且N是线段AM的中点,若AB=14cm,BM=6cm,则AN的长为( )| A、3cm | B、4cm |
| C、6cm | D、7cm |
 如图是一个底面三边长都是3cm三棱柱,它的侧面是正方形.现要从中挖取一个底面最大的圆柱.
如图是一个底面三边长都是3cm三棱柱,它的侧面是正方形.现要从中挖取一个底面最大的圆柱.