题目内容
7.已知关于x的方程x2-(a+b)x+ab-1=0,x1、x2是此方程的两个实数根,现给出四个结论:①x1≠x2;②x1x2<ab;③x12+x22>a2+b2;④若a>b,x1>x2,则x1-x2=a-b,则正确结论的序号是①②③.(填上你认为正确结论的所有序号)分析 ①根据方程的系数结合根的判别式即可得出△=(a-b)2+4>0,由此即可得出x1≠x2,结论①成立;②由根与系数的关系即可得出x1x2=ab-1,由此即可得出x1x2<ab,结论②成立;③由根与系数的关系可得出x1+x2=a+b、x1x2=ab-1,将x12+x22变形为$({x}_{1}+{x}_{2})^{2}$-2x1x2,代入数据即可得出x12+x22=a2+b2+2,进而可得出x12+x22>a2+b2,结论③成立;④结合③中的x12+x22=a2+b2+2以及x1+x2=a+b、x1x2=ab-1即可得出${(x}_{1}-{x}_{2})^{2}$=(a-b)2+4,由此即可得出${(x}_{1}-{x}_{2})^{2}$>(a-b)2,再根据a>b、x1>x2,即可得出x1-x2>a-b,结论④不成立.综上即可得出结论.
解答 解:①∵在方程x2-(a+b)x+ab-1=0中,△=[-(a+b)]2-4(ab-1)=a2+b2+2ab-4ab+4=(a-b)2+4>0,
∴x1≠x2,结论①成立;
②∵x1、x2是方程x2-(a+b)x+ab-1=0的两个实数根,
∴x1x2=ab-1<ab,结论②成立;
③∵x1、x2是方程x2-(a+b)x+ab-1=0的两个实数根,
∴x1+x2=a+b,x1x2=ab-1,
∴x12+x22=$({x}_{1}+{x}_{2})^{2}$-2x1x2=(a+b)2-2(ab-1)=a2+b2+2ab-2ab+2=a2+b2+2>a2+b2,结论③成立;
④∵x1+x2=a+b,x1x2=ab-1,
∴${(x}_{1}-{x}_{2})^{2}$=x12+x22-2x1x2=a2+b2+2-2(ab-1)=(a-b)2+4,
∴${(x}_{1}-{x}_{2})^{2}$>(a-b)2.
又∵a>b,x1>x2,
∴x1-x2>a-b,结论④不成立.
故答案为:①②③.
点评 本题考查了根与系数的关系、根的判别式以及完全平方公式,逐一分析四条结论是否成立是解题的关键.

| A. | 4 | B. | 8 | C. | ±4 | D. | ±8 |
| A. | 20 | B. | -16 | C. | 20或-16 | D. | -20或16 |
| A. | 1:3 | B. | 1:9 | C. | 3:1 | D. | 9:1 |
| 加数的个数n | 和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
(2)根据表中的规律猜想:用n的代数式表示和S的公式为:S=2+4+6+8+…+2n=n(n+1);
(3)计算:34+36+38+…+108的值.
 如图,在平面直角坐标系中,把直线y=3x沿y轴向下平移后得到直线AB,如果点N(m,n)是直线AB上的一点,且3m-n=2,那么直线AB的函数表达式为y=3x-2.
如图,在平面直角坐标系中,把直线y=3x沿y轴向下平移后得到直线AB,如果点N(m,n)是直线AB上的一点,且3m-n=2,那么直线AB的函数表达式为y=3x-2.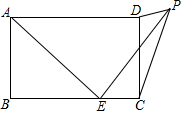 如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长为3或$\frac{5+\sqrt{17}}{2}$.
如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长为3或$\frac{5+\sqrt{17}}{2}$.