题目内容
11.某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
分析 (1)根据售量y(件)与售价x(元/件)之间的函数关系即可得到结论;
(2))设每星期利润为y元,构建二次函数利用二次函数性质解决问题.
解答 解:(1)根据题意可得:
y=300+30(60-x)
=-30x+2100;
(2)设每星期利润为W元,根据题意可得:
W=(x-40)(-30x+2100)
=-30(x-55)2+6750.
则x=55时,W最大值=6750.
故每件售价定为55元时,每星期的销售利润最大,最大利润6750元.
点评 本题考查二次函数的应用,解题的关键是构建二次函数解决最值问题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
1.下列代数式的书写规范的是( )
| A. | m×n | B. | 7ab÷6 | C. | 2$\frac{1}{3}$x | D. | a2-$\frac{1}{a}$ |
 如图,四个有理数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若n+q=0,则m,n,p,q四个有理数中,绝对值最小的一个是( )
如图,四个有理数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若n+q=0,则m,n,p,q四个有理数中,绝对值最小的一个是( ) 如图,已知△ABC,用直尺(没有刻度)和圆规在平面上求作一个点P,使P到∠B两边的距离相等,且PA=PB.(不要求写作法,但要保留作图痕迹)
如图,已知△ABC,用直尺(没有刻度)和圆规在平面上求作一个点P,使P到∠B两边的距离相等,且PA=PB.(不要求写作法,但要保留作图痕迹) 已知△ABC,请在△ABC内确定一个点P,使得点P到AB和BC的距离相等,且满足P到点A和点C的距离相等.(不写作法,保留作图痕迹).
已知△ABC,请在△ABC内确定一个点P,使得点P到AB和BC的距离相等,且满足P到点A和点C的距离相等.(不写作法,保留作图痕迹).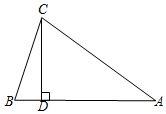 已知△ABC中,AB=AC,CD⊥AB于D.
已知△ABC中,AB=AC,CD⊥AB于D.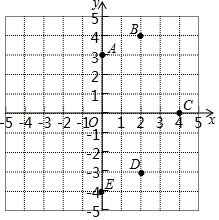 如图,在平面直角坐标系中,已知点A(0,3),B(2,4),C(4,0),D(2,-3),E(0,-4).
如图,在平面直角坐标系中,已知点A(0,3),B(2,4),C(4,0),D(2,-3),E(0,-4).