题目内容
19.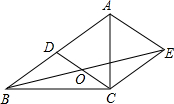 如图,在Rt△ABC中,∠ACB=90°,AD=BD,AE∥CD,CE∥AB,BE交CD于O.
如图,在Rt△ABC中,∠ACB=90°,AD=BD,AE∥CD,CE∥AB,BE交CD于O.(1)判断四边形ADCE的形状,并证明.
(2)若AC=BC=2,求BO的长.
分析 (1)首先证得四边形ADCE是平行四边形,然后证得邻边相等即可得到菱形;
(2)首先根据AC=BC=2得到CD⊥AB,AB=2$\sqrt{2}$,从而得到AE=$\sqrt{2}$,然后利用勾股定理求得BE=$\sqrt{10}$,从而求得BO=$\frac{1}{2}$BE=$\frac{\sqrt{10}}{2}$.
解答 解:(1)菱形.证明如下:
∵AE∥CD,CE∥AD,
∴四边形ADCE是平行四边形,
∵∠ACB=90°,AD=BD,
∴CD=AD,
∴四边形ADCE是菱形.
(2)∵AC=BC=2,
∴CD⊥AB,AB=2$\sqrt{2}$,
∴EA⊥AB,AD=$\sqrt{2}$,
∴AE=$\sqrt{2}$,
在Rt△BAE中,BE=$\sqrt{(2\sqrt{2})^{2}+(\sqrt{2})^{2}}$=$\sqrt{10}$,
∵AD=BD,AE∥DO,
∴BO=$\frac{1}{2}$BE=$\frac{\sqrt{10}}{2}$.
点评 本题考查了菱形的判定及勾股定理的知识,解题的关键是牢记菱形的判定定理,难度不大.

练习册系列答案
相关题目
10.以三角形三边中点和三角形三个顶点能画出平行四边形有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
7.比3大-1的数是( )
| A. | 2 | B. | 4 | C. | -3 | D. | -2 |
14.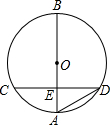 如图,已知AB是圆O的直径,弦CD⊥AB,垂足为E,连接AD,AB=9,AD=6,则弦CD的长为( )
如图,已知AB是圆O的直径,弦CD⊥AB,垂足为E,连接AD,AB=9,AD=6,则弦CD的长为( )
 如图,已知AB是圆O的直径,弦CD⊥AB,垂足为E,连接AD,AB=9,AD=6,则弦CD的长为( )
如图,已知AB是圆O的直径,弦CD⊥AB,垂足为E,连接AD,AB=9,AD=6,则弦CD的长为( )| A. | 4$\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
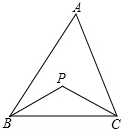 如图,P是△ABC内任一点,
如图,P是△ABC内任一点,