题目内容
11.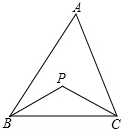 如图,P是△ABC内任一点,
如图,P是△ABC内任一点,(1)试说明∠BPC>∠A.
(2)若∠ABC=80°,∠ACB=50°,BP平分∠ABC,CP平分∠ACB,求∠BPC的度数.
(3)若∠BPC=130°,试求∠A的度数.
分析 (1)如图,延长BP交AC于D.根据△PDC外角的性质知∠BPC>∠PDC;根据△ABD外角的性质知∠PDC>∠A,所以易证∠BPC>∠A;
(2)利用三角形角平分线性质得:∠CBP=$\frac{1}{2}$∠ABC=40°,∠BCP=$\frac{1}{2}$∠ACB=25°;由三角形的内角和定理,求得∠BPC的度数;
(3)先根据三角形内角和定理求出∠PBC+∠PCB的度数,再根据角平分线的性质求出∠ABC+∠ACB的度数,由三角形内角和定理即可求出答案.
解答 (1)证明:如图,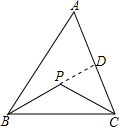
延长BP交AC于D.
∵∠BPC>∠PDC,∠PDC>∠A,
∴∠BPC>∠A.
(2)解:在△ABC中,
∵∠ABC=80°,BP平分∠ABC,
∴∠CBP=$\frac{1}{2}$∠ABC=40°.
∵∠ACB=50°,CP平分∠ACB,
∴∠BCP=$\frac{1}{2}$∠ACB=25°.
在△BCP中∠BPC=180°-(∠CBP+∠BCP)=115.
(3)解:∠PBC+∠PCB+∠BPC=180°,
∵∠BPC=130°,
∴∠PBC+∠PCB=50°,
∵BP、CP是角平分线,
∴∠ABC=2∠PBC,∠ACB=2∠PCB,
∴∠ABC+∠ACB=100°,
∵∠ABC+∠ACB+∠A=180°,
∴∠A=80°.
点评 本题考查了三角形的外角的性质、三角形角平分线性质及三角形的内角和定理.解题时是结合三角形的内角和与外角的关系、角平分线的性质来证明结论的.

练习册系列答案
相关题目
2.如图电视台的标志中,属于中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.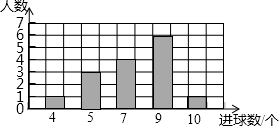 某篮球兴趣小组有15名同学,在一次投篮比赛中,他们的成绩如右面的条形图所示.这15名同学进球数的众数和中位数分别是( )
某篮球兴趣小组有15名同学,在一次投篮比赛中,他们的成绩如右面的条形图所示.这15名同学进球数的众数和中位数分别是( )
 某篮球兴趣小组有15名同学,在一次投篮比赛中,他们的成绩如右面的条形图所示.这15名同学进球数的众数和中位数分别是( )
某篮球兴趣小组有15名同学,在一次投篮比赛中,他们的成绩如右面的条形图所示.这15名同学进球数的众数和中位数分别是( )| A. | 10,7 | B. | 7,7 | C. | 9,9 | D. | 9,7 |
1.下列调查中,适合用普查方法的是( )
| A. | 了解某班学生对“五城联创”的知晓率 | |
| B. | 了解某种奶制品中蛋白质的含量 | |
| C. | 了解十堰台《十堰新闻》栏目的收视率 | |
| D. | 了解一批节能灯的使用寿命 |
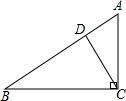 如图所示,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,CD⊥AB于点D.求∠BCD的三个三角函数值.
如图所示,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,CD⊥AB于点D.求∠BCD的三个三角函数值.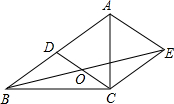 如图,在Rt△ABC中,∠ACB=90°,AD=BD,AE∥CD,CE∥AB,BE交CD于O.
如图,在Rt△ABC中,∠ACB=90°,AD=BD,AE∥CD,CE∥AB,BE交CD于O.