题目内容
9.已知线段AB=12cm,C为直线AB上任一点,点M、N分别是AC、BC的中点,那么MN=6cm.如果AM=4cm,那么BN=2cm.分析 根据题意,分三种情况:(1)当C在A、B之间时;(2)当C在线段AB的延长线上时;(3)当C在线段BA的延长线上时;然后根据点M、N分别是AC、BC的中点,求出MN、BN的长度各是多少即可.
解答 解:∵M是线段AC的中点,
∴CM=$\frac{1}{2}$AC,
∵N是线段BC的中点,
∴CN=$\frac{1}{2}$BC,
(1)如图1, ,
,
当C在A、B之间时,
∵点M、N分别是AC、BC的中点,
∴AM=CM,CN=BN,
∴MN=CM+CN=$\frac{1}{2}$AB=$\frac{1}{2}×12=6(cm)$,
(2)如图2, ,
,
当C在线段AB的延长线上时,
∵点M、N分别是AC、BC的中点,
∴AM=CM,CN=BN,
∴MN=CM-CN=$\frac{1}{2}AC-\frac{1}{2}BC$=$\frac{1}{2}$AB=$\frac{1}{2}×12=6(cm)$,
(3)如图3, ,
,
当C在线段BA的延长线上时,
MN=CN-CM=$\frac{1}{2}BC-\frac{1}{2}AC=\frac{1}{2}AB$=$\frac{1}{2}×12=6(cm)$,
∵AM=4cm,
∴BN=(12-4×2)÷2=2(cm).
综上,可得MN=6cm,BN=2cm.
故答案为:6、2.
点评 此题主要考查了两点间的距离的求法,考查了分类讨论思想的应用,要熟练掌握,解答此题的关键是要明确:连接两点间的线段的长度叫两点间的距离.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
3. 统计七年级部分同学的跳高测试成绩,得到如下频数直方图(每组含前一个边界值,不含后一个边界值),其中规定成绩在1.29m及以上的为优秀,由此得到的信息错误的是( )
统计七年级部分同学的跳高测试成绩,得到如下频数直方图(每组含前一个边界值,不含后一个边界值),其中规定成绩在1.29m及以上的为优秀,由此得到的信息错误的是( )
 统计七年级部分同学的跳高测试成绩,得到如下频数直方图(每组含前一个边界值,不含后一个边界值),其中规定成绩在1.29m及以上的为优秀,由此得到的信息错误的是( )
统计七年级部分同学的跳高测试成绩,得到如下频数直方图(每组含前一个边界值,不含后一个边界值),其中规定成绩在1.29m及以上的为优秀,由此得到的信息错误的是( )| A. | 参加测试的总人数为54人 | |
| B. | 组距为0.10m | |
| C. | 该测试优秀率为60% | |
| D. | 组中值为1.14m的组的边界值分别为1.09m与1.19m |
20.一组数据的最大值为100,最小值为61,若组距为6,则这组数据可分成( )
| A. | 5组 | B. | 6组 | C. | 7组 | D. | 8组 |
4.在下列实数中,无理数是( )
| A. | 0 | B. | π | C. | 0.101101110 | D. | sin30° |
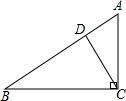 如图所示,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,CD⊥AB于点D.求∠BCD的三个三角函数值.
如图所示,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,CD⊥AB于点D.求∠BCD的三个三角函数值.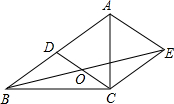 如图,在Rt△ABC中,∠ACB=90°,AD=BD,AE∥CD,CE∥AB,BE交CD于O.
如图,在Rt△ABC中,∠ACB=90°,AD=BD,AE∥CD,CE∥AB,BE交CD于O.