题目内容
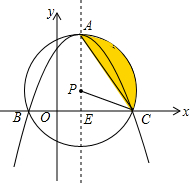 如图,已知抛物线y=ax2+bx+c(a<0)的顶点A在以P(1,1)为圆心,2为半径的圆上,且经过⊙P与x轴的两个交点B、C,AP⊥x轴于点E.
如图,已知抛物线y=ax2+bx+c(a<0)的顶点A在以P(1,1)为圆心,2为半径的圆上,且经过⊙P与x轴的两个交点B、C,AP⊥x轴于点E.(1)求抛物线的解析式;
(2)求⊙P的弦AC在第一象限内形成的弓形(阴影部分)的面积;
(3)在抛物线上能否找到一点D,使线段DP与OA互相平分?如果能,求出D点坐标,如果不能,请说明理由.
考点:二次函数综合题
专题:
分析:(1)根据B、C两点在⊙P上,在Rt△BPE与Rt△CPE中,得出PB=PC=2,EP=1,进而求出B,C的坐标;利用交点式求出二次函数解析式即可;
(2)首先利用锐角三角函数关系得出∠APC的度数,进而利用S阴影=S扇形APC+S△PEC-S△AEC求出即可;
(3)根据若满足条件的点D存在,四边EADO一定是平行四边形,也即一定有AE∥OD,OD=AE,由AE∥OD,可知点D在y轴上,又知D在抛物线y=-(x-1)2+3上,即可的求出.
(2)首先利用锐角三角函数关系得出∠APC的度数,进而利用S阴影=S扇形APC+S△PEC-S△AEC求出即可;
(3)根据若满足条件的点D存在,四边EADO一定是平行四边形,也即一定有AE∥OD,OD=AE,由AE∥OD,可知点D在y轴上,又知D在抛物线y=-(x-1)2+3上,即可的求出.
解答:解:(1)依题意AE⊥x轴,则点A的坐标为(1,3)
连接PB,
∵B、C两点在⊙P上,在Rt△BPE与Rt△CPE中,
∵PB=PC=2,PE=1,
∴BE=EC=
,
∴OB=BE-EO=
-1;OC=OE+EC=1+
,
∴B(2-
,0),C(1+
,0);
根据交点式,设抛物线的解析式为:y=a(x-1+
)(x-1-
),
又∵点A(1,3)在抛物线上,
∴3=a(1-1+
)(1-1-
),
解得:a=-1,
故抛物线的解析式为:y=-(x-1)2+3,
即y=-x2+2x+2,
(2)∵EP=1,PC=2,PE⊥EC,
∴∠PEC=60°,
∴∠APC=120°,
∴S阴影=S扇形APC+S△PEC-S△AEC=
+
×1×
-
×
×3=
-
;
(3)满足条件的D点存在.
若满足条件的点D存在,四边形PADO一定是平行四边形,也即一定有AP∥OD,OD=AP,
由AP∥OD,可知点D在y轴上,又知D在抛物线y=-(x-1)2+3上,
可令x=0,得y=2,
∴D(0,2),
此时恰好OD=AP=2,
所以D(0,2)为所求.
连接PB,
∵B、C两点在⊙P上,在Rt△BPE与Rt△CPE中,
∵PB=PC=2,PE=1,
∴BE=EC=
| 3 |
∴OB=BE-EO=
| 3 |
| 3 |
∴B(2-
| 3 |
| 3 |
根据交点式,设抛物线的解析式为:y=a(x-1+
| 3 |
| 3 |
又∵点A(1,3)在抛物线上,
∴3=a(1-1+
| 3 |
| 3 |
解得:a=-1,
故抛物线的解析式为:y=-(x-1)2+3,
即y=-x2+2x+2,

(2)∵EP=1,PC=2,PE⊥EC,
∴∠PEC=60°,
∴∠APC=120°,
∴S阴影=S扇形APC+S△PEC-S△AEC=
| 120π×22 |
| 360 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4π |
| 3 |
| ||
| 2 |
(3)满足条件的D点存在.
若满足条件的点D存在,四边形PADO一定是平行四边形,也即一定有AP∥OD,OD=AP,
由AP∥OD,可知点D在y轴上,又知D在抛物线y=-(x-1)2+3上,
可令x=0,得y=2,
∴D(0,2),
此时恰好OD=AP=2,
所以D(0,2)为所求.
点评:此题主要考查了直角三角形的性质以及交点式求二次函数解析式,以及平行四边形的性质,综合性强,能力要求极高.考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下面计算正确的是( )
| A、3x2-2x2=3 | ||
| B、3a2+2a3=5a5 | ||
| C、3+x=3x | ||
D、-0.25ab+
|
把方程x2-8x+3=0配方成如下的形式,则正确是( )
| A、(x+4)2=13 |
| B、(x-4)2=19 |
| C、(x-4)2=13 |
| D、(x+4)2=19 |
在下列实数中,无理数是( )
A、
| ||
B、
| ||
C、-
| ||
| D、0 |