题目内容
已知直线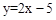 与x轴和y轴分别交于点A和点B,抛物线
与x轴和y轴分别交于点A和点B,抛物线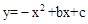 的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
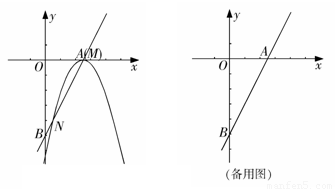
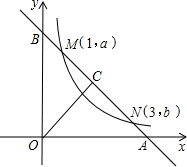
(1)如图,当点M与点A重合时,求:
①抛物线的解析式;(4分)
②点N的坐标和线段MN的长;(4分)
(2)抛物线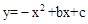 在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.(4分)
在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.(4分)
【答案】
(1)①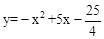 ②N(
②N(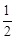 ,-4),
,-4),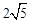 (2)存在。点M的坐标为(2,-1)或(4,3)
(2)存在。点M的坐标为(2,-1)或(4,3)
【解析】解:(1)①∵直线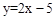 与x轴和y轴分别交于点A和点B,∴A(
与x轴和y轴分别交于点A和点B,∴A(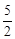 ,0),B(0,-5)。
,0),B(0,-5)。
当顶点M与点A重合时,∴M(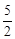 ,0)。
,0)。
∴抛物线的解析式是: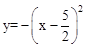 ,即
,即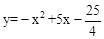 。
。
②∵N是直线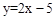 与在抛物线
与在抛物线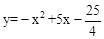 的交点,
的交点,
∴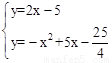 ,解得
,解得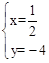 或
或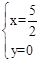 。
。
∴N(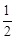 ,-4)。
,-4)。
如图,过N作NC⊥x轴,垂足为C。
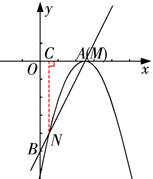
∵N(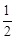 ,-4),∴C(
,-4),∴C(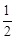 ,0)
,0)
∴NC=4.MC=OM-OC=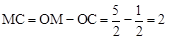 。
。
∴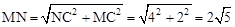 。
。
(2)存在。点M的坐标为(2,-1)或(4,3)。
(1)①由直线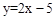 与x轴和y轴分别交于点A和点B,求出点A、B的坐标,由顶点M与点A重合,根据二次函数的性质求出顶点解析式。
与x轴和y轴分别交于点A和点B,求出点A、B的坐标,由顶点M与点A重合,根据二次函数的性质求出顶点解析式。
②联立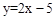 和
和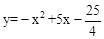 ,求出点N的坐标,过N作NC⊥x轴,由勾股定理求出线段MN的长。
,求出点N的坐标,过N作NC⊥x轴,由勾股定理求出线段MN的长。
(2)存在两种情况,△OMN与△AOB相似:
情况1,∠OMN=900,过M作MD⊥x轴,垂足为D。

设M(m,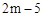 ),则OD= m,DM=
),则OD= m,DM=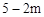 。
。
又OA=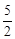 ,OB=5,
,OB=5,
则由△OMD∽△BAO得,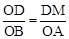 ,即
,即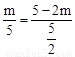 ,解得m=2。
,解得m=2。
∴M(2,-1)。
情况2,
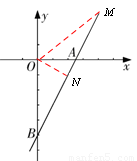
∠ONM=900,若△OMN与△AOB相似,则∠OMN=∠OBN。
∴OM=OB=5。
设M(m,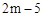 ),则
),则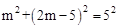 解得m=4。
解得m=4。
∴M(4,3)。
综上所述,当点M的坐标为(2,-1)或(4,3)时,△OMN与△AOB相似。

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 与x轴和y轴分别相交于点A和B,OC⊥AB,垂足为C.
与x轴和y轴分别相交于点A和B,OC⊥AB,垂足为C. 如图所示,已知直线与x轴、y轴分别交于A、B两点,并且与反比例函数
如图所示,已知直线与x轴、y轴分别交于A、B两点,并且与反比例函数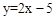 与x轴和y轴分别交于点A和点B,抛物线
与x轴和y轴分别交于点A和点B,抛物线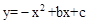 的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.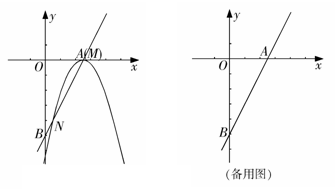
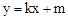 与x轴、y轴分别交于A、C两点,抛物线
与x轴、y轴分别交于A、C两点,抛物线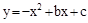 经过A、C两点,点B是抛物线与x轴的另一个交点,当
经过A、C两点,点B是抛物线与x轴的另一个交点,当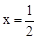 时,y取最大值
时,y取最大值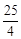 .
.
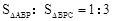 ,求点P的坐标;
,求点P的坐标;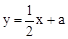 与(1)中所求的抛物线交于M、N两点,问:
与(1)中所求的抛物线交于M、N两点,问: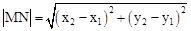 )
)