题目内容
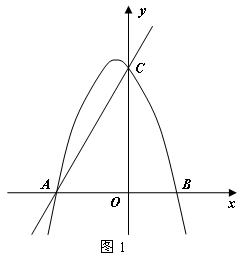
如图1所示,已知直线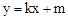 与x轴、y轴分别交于A、C两点,抛物线
与x轴、y轴分别交于A、C两点,抛物线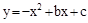 经过A、C两点,点B是抛物线与x轴的另一个交点,当
经过A、C两点,点B是抛物线与x轴的另一个交点,当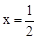 时,y取最大值
时,y取最大值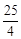 .
.

(1)求抛物线和直线的解析式;
(2)设点P是直线AC上一点,且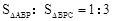 ,求点P的坐标;
,求点P的坐标;
(3)若直线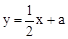 与(1)中所求的抛物线交于M、N两点,问:
与(1)中所求的抛物线交于M、N两点,问:
①是否存在a的值,使得∠MON=900?若存在,求出a的值;若不存在,请说明理由;
②猜想当∠MON>900时,a的取值范围(不写过程,直接写结论).
(参考公式:在平面直角坐标系中,若M(x1,y1),N(x2,y2),则M,N两点间的距离为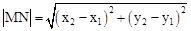 )
)
(1) (2)
(2) 或
或 (3)①存在②当
(3)①存在②当 时,∠MON>900。
时,∠MON>900。
【解析】解:(1)∵当 时,
时, 取最大值
取最大值 ,
,
∴ ,解得
,解得 。
。
∴抛物线的解析式为 。
。
令 ,解得
,解得 ,∴A(-3,0),B(2,0)。
,∴A(-3,0),B(2,0)。
令x=0,得 ,∴C(0,6)。
,∴C(0,6)。
将A、C的坐标代入 ,得
,得
 ,解得
,解得 。
。
∴直线AC的解析式为 。
。
(2)分两种情况:
①点P在线段AC上时,过P作PH⊥x轴,垂足为H,

∵ ,∴
,∴ 。
。
∵PH∥CP,∴△APH∽△ACO。
∴ ,即
,即 。
。
∴ 。∴
。∴ 。
。
∴ 。
。
②点P在线段CA的延长线上时,过P作PG⊥x轴,垂足为G,

∵ ,∴
,∴ 。
。
∵PG∥CO,∴△APG∽△ACO。
∴ ,即
,即 。
。
∴ 。∴
。∴ 。
。
∴ 。
。
综上所述,点P的坐标为 或
或 。
。
(3)①存在。
假设存在a的值,使直线 与(1)中所求的抛物线
与(1)中所求的抛物线 交于M(x1,y1),N(x2,y2)两点(M在N的左侧),使得∠MON=900,
交于M(x1,y1),N(x2,y2)两点(M在N的左侧),使得∠MON=900,
由 得
得 。
。
∴ 。
。
又 ,
, ,
,
∴ 。
。
∵∠MON=900,∴ 。
。
∴ 。∴
。∴ 。
。
∴ ,即
,即 ,解得
,解得 或
或 。
。
∴存在 或
或 使得∠MON=900。
使得∠MON=900。
②当 时,∠MON>900。
时,∠MON>900。
(1)根据当 时,
时, 取最大值
取最大值 列式求出b、c,从而得到抛物线的解析式;由抛物线的解析式得到A,C的坐标,由待定系数法求出直线AC的解析式。
列式求出b、c,从而得到抛物线的解析式;由抛物线的解析式得到A,C的坐标,由待定系数法求出直线AC的解析式。
(2)分点P在线段AC上和两种情况讨论即可。
(3)①应用一元二次方程根与系数的关系和勾股定理求解。
②如图,

当 或
或 时,∠MON=900;
时,∠MON=900;
当 或
或 时,∠MON<900;
时,∠MON<900;
当 时,∠MON>900。
时,∠MON>900。

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案 ,
, ,
, ,则
,则 的度数为
的度数为
A.70 | B.80 | C.90 | D.100 |
 (2013•黄石)如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-
(2013•黄石)如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-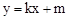 与x轴、y轴分别交于A、C两点,抛物线
与x轴、y轴分别交于A、C两点,抛物线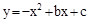 经过A、C两点,点B是抛物线与x轴的另一个交点,当
经过A、C两点,点B是抛物线与x轴的另一个交点,当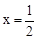 时,y取最大值
时,y取最大值 .
.
 ,求点P的坐标;
,求点P的坐标;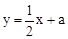 与(1)中所求的抛物线交于M、N两点,问:
与(1)中所求的抛物线交于M、N两点,问: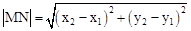 )
) 如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-
如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=- 时,y取最大值
时,y取最大值 .
. x+a与(1)中所求的抛物线交于点M、N,两点,问:
x+a与(1)中所求的抛物线交于点M、N,两点,问: )
) ,
, ,
, ,则
,则 的度数为
的度数为
 B.80
B.80