题目内容
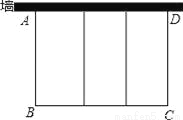
如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
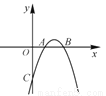
已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.
已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
查看答案已知关于x的方程x2+ax+a-2=0.
(1)若该方程的一个根为1,求a的值及该方程的另一个根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
查看答案用适当的方法解下列方程.
①(2x+3)2﹣16=0;
②2x2=3(2x+1).
查看答案如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+4上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为____.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案某市居民用电的电价实行阶梯收费,收费标准如下表:
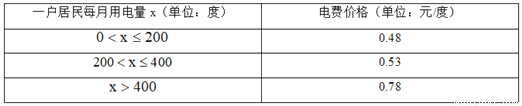
七月份是用电高峰期,李叔计划七月份电费支出不超过200元,直接写出李叔家七月份最多可用电的度数是( )
A. 100 B. 396 C. 397 D. 400
B 【解析】设李叔家七月份最多可用电x度, 根据题意得:200×0.48+0.53(x?200)?200, 解得:x?396.2. 故李叔家六月份最多可用电396度。 故选:B将直尺和直角三角板按如图方式摆放(∠ACB为直角),已知∠1=30°,则∠2的大小是( )
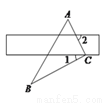
A. 30° B. 45° C. 60° D. 65°
查看答案小文统计了本班同学一周的体育锻练情况,并绘制了直方图
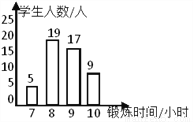
①小文同学一共统计了60人;
②这个班同学一周参加体育锻炼时间的众数是8;
③这个班同学一周参加体育锻炼时间的中位数是9;
④这个班同学一周参加体育锻炼时间的平均值为8.
根据图中信息,上述说法中正确的是( )
A. ①② B. ②③ C. ③④ D. ①④
查看答案下列因式分解正确的是( )
A. 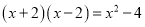 B.
B. 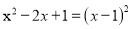
C. 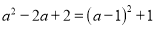 D.
D. 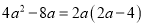
若把不等式x+2≤0的解集在数轴上表示出来,则正确的是( )
A.  B.
B. 
C. 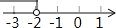 D.
D. 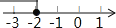
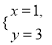 是二元一次方程
是二元一次方程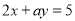 的一个解,则a的值为( )
的一个解,则a的值为( )
A. 1 B. 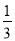 C. 3 D. -1
C. 3 D. -1
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知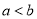 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
A. 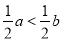 B.
B. 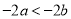 C.
C. 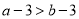 D.
D. 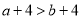
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,2.5微米等于0.0000025米,把0.0000025用科学记数法表示为( )
A. 2.5×106 B. 0.25×10-5 C. 2.5×10-6 D. 25×10-7
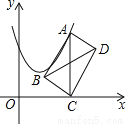
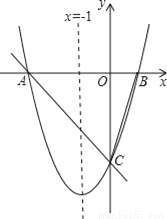
查看答案如图,对称轴为x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).
(1)求点B的坐标.
(2)已知a=1,C为抛物线与y轴的交点.
①若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标.
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
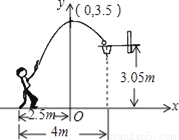
查看答案宜昌四中男子篮球队在2016全区篮球比赛中蝉联冠军,让全校师生倍受鼓舞.在一次与第25中学的比赛中,运动员小涛在距篮下4米处跳起投篮,如图所示,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
(1)建立如图所示的直角坐标系,求抛物线的表达式;
(2)运动员小涛的身高是1.8米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,小涛跳离地面的高度是多少?
如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?

- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1,y2,y3的大小关系为( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y2>y1 D. y3>y1>y2
A 【解析】试题解析:∵函数的解析式是y=-(x+1)2+3, ∴对称轴是x=-1, ∴点A关于对称轴的点A′是(0,y1), 那么点A′、B、C都在对称轴的右边,而对称轴右边y随x的增大而减小, 于是y1>y2>y3. 故选A.在同一坐标系中,一次函数y=-mx+n2与二次函数y=x2+m的图象可能是( )
A.  B.
B.  C.
C.  D.
D. 
关于x的一元二次方程x2﹣3x+m=0没有实数根,则实数m的取值范围为( )
A.  B.
B.  C.
C.  D.
D. 
抛物线y=3x2+2x-1向上平移4个单位长度后的函数解析式为( )
A. y=3x2+2x-5 B. y=3x2+2x-4 C. y=3x2+2x+3 D. y=3x2+2x+4
查看答案要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场,根据时间和场地等条件,赛程计划安排7天,每天安排4场比赛,设比赛组织者应邀请x个队参赛,则x满足的关系式为( )
A.  x(x+1)=28 B.
x(x+1)=28 B.  x(x-1)=28 C. x(x+1)=28 D. x(x-1)=28
x(x-1)=28 C. x(x+1)=28 D. x(x-1)=28
已知x1、x2是一元二次方程x2﹣4x+1=0的两个根,则x1+x2等于( )
A.﹣4 B.﹣1 C.1 D.4
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
若x2+x=2,则(x2+2x)﹣(x+1)值是_____.
1 【解析】(x2+2x)-(x+1)=x2+2x-x-1= x2+x-1=2-1=1. 故答案为1.如果(x+3)2+|y﹣2|=0,则xy=_____.
查看答案如图所示的运算程序中,若开始输入的x值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…第2017次输出的结果为( )
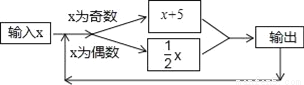
A. 3 B. 6 C. 4 D. 2
查看答案下列是由一些火柴搭成的图案:图①用了5根火柴,图②用了9根火柴,图③用了13根火柴,按照这种方式摆下去,摆第5个图案用多少根火柴棒( )
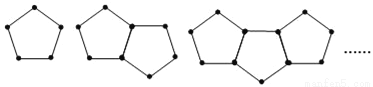
A. 20 B. 21 C. 22 D. 23
查看答案多项式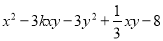 合并同类项后不含xy项,则k的值是( )
合并同类项后不含xy项,则k的值是( )
A. 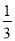 B.
B. 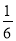 C.
C. 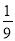 D. 0
D. 0
如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )
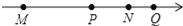
A. 点M B. 点N C. 点P D. 点Q
查看答案 试题属性- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知一组数据:16,15,16,14,17,16,15,则众数是( )
A. 17 B. 16 C. 15 D. 14
B 【解析】∵在这组数据中16出现的次数最多, ∴这组数据的众数是16. 故选B.已知⊙O的半径为2,直线l上有一点P满足PO=2,则直线l与⊙O的位置关系是( )
A. 相切 B. 相离 C. 相离或相切 D. 相切或相交
查看答案方程:x(x+1)=3(x+1)的解的情况是( )
A.x=﹣1 B.x=3 C.x1=﹣1,x2=3 D.以上答案都不对
查看答案已知:m,x,y满足:(1) ;(2)﹣2a2by+1与7b3a2是同类项.
;(2)﹣2a2by+1与7b3a2是同类项.
求代数式:2x2﹣6y2+m(xy﹣9y2)﹣(3x2﹣3xy+7y2)的值.
查看答案某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶情况记录如下(单位:千米):+10,﹣8,+7,﹣15,+6,﹣16,+4,﹣2
(1)A处在岗亭何方?距离岗亭多远?
(2)若摩托车每行驶1千米耗油0.5升,这一天共耗油多少升?
查看答案化简求值:(2x2y﹣4xy2)﹣(﹣3xy2+x2y),其中x=﹣1,y=2.
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧

