题目内容
2. 在美化城市的建设中,某街道想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设BC=xm.
在美化城市的建设中,某街道想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设BC=xm.(1)若花园的面积为195m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是6m和8m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S(m2)的最大值.
分析 (1)根据题意表示出矩形的边AB的长,根据矩形面积=长×宽列出方程,求解可得;
(2)根据P与墙CD,AD的距离分别是6m和8m确定自变量x的取值范围,将(1)中函数关系式配方再结合x的取值范围可得S的最大值.
解答 解:(1)根据题意,BC=xm,则AB=(28-x)m,
故x(28-x)=195,
解得:x=13或x=15;
(2)∵P与墙CD,AD的距离分别是6m和8m,
∴x≥6且28-x≥8,解得:6≤x≤20,
由题意可得:S=x(28-x)=-x2+28x=-(x-14)2+196,
∴当x=14时,S取得最大值,最大值为196,
答:花园面积S的最大值为196m2.
点评 本题主要考查了解一元二次方程的基本素质和二次函数性质求最值的能力,根据相等关系列出方程或解析式是基础,确定自变量范围并结合范围确定最值是关键.

练习册系列答案
相关题目
7.下列几组数中,为勾股数的是( )
| A. | $\frac{3}{5}$,$\frac{4}{5}$,1 | B. | 3,4,6 | C. | 5,12,13 | D. | 0.9,1.2,1.5 |
11.不等式组$\left\{\begin{array}{l}x+3>0\\ x-3≤0\end{array}\right.$的解集是( )
| A. | x>-3 | B. | x≤3 | C. | -3<x≤3 | D. | x≥3 |
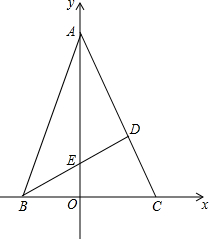 如图,在坐标系中,A(0,6),B(-2,0),C(3,0),∠BAC=45°,BD⊥AC,M(4,6),动点P从点M出发,沿x轴正方向,以每秒2个单位的长度运动t秒
如图,在坐标系中,A(0,6),B(-2,0),C(3,0),∠BAC=45°,BD⊥AC,M(4,6),动点P从点M出发,沿x轴正方向,以每秒2个单位的长度运动t秒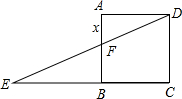 如图,边长为1的正方形ABCD中,点E在CB延长线上,连接ED交A8于点F,AF=x(0.2≤x≤0.8),EC=y.则大致能反映y与x之闻函数关系的是y=$\frac{1}{x}$.
如图,边长为1的正方形ABCD中,点E在CB延长线上,连接ED交A8于点F,AF=x(0.2≤x≤0.8),EC=y.则大致能反映y与x之闻函数关系的是y=$\frac{1}{x}$. 如图,直线AB和CD相交于点0,则∠AOD=∠BOC.
如图,直线AB和CD相交于点0,则∠AOD=∠BOC.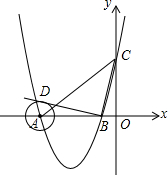 如图,在平面直角坐标系中,顶点为(-3,-4)的抛物线交x轴于A、B两点(点A在点B的左侧),交y轴于C点,已知C点坐标为(0,5).
如图,在平面直角坐标系中,顶点为(-3,-4)的抛物线交x轴于A、B两点(点A在点B的左侧),交y轴于C点,已知C点坐标为(0,5).