题目内容
12. (1)如图,正方形网格中每个小正方形边长都是1,每个小格顶点称为格点,以格点为顶点画一个三角形使三角形的三边长分别为$\sqrt{5}$,$\sqrt{5}$,$\sqrt{10}$
(1)如图,正方形网格中每个小正方形边长都是1,每个小格顶点称为格点,以格点为顶点画一个三角形使三角形的三边长分别为$\sqrt{5}$,$\sqrt{5}$,$\sqrt{10}$(2)你所画的三角形是直角三角形(填“是”或“不是”);
(3)你画的三角形的面积为$\frac{5}{2}$.
分析 (1)如图△ABC即为所求;
(2)利用勾股定理的逆定理即可判断;
(3)根据S△ABC=$\frac{1}{2}$•AB•BC计算即可;
解答 解:(1)如图△ABC即为所求.(AB=BC=$\sqrt{5}$,AC=$\sqrt{10}$)
(2)∵AB2+BC2=AC2,
∴△ABC是直角三角形,
故答案为是.
(3)S△ABC=$\frac{1}{2}$•AB•BC=$\frac{5}{2}$.
故答案为$\frac{5}{2}$.
点评 本题考查作图-应用与设计、勾股定理、勾股定理的逆定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
3.若a、b、c为△ABC的三边长,且满足|a-4|+(b-2)2=0,则c的值可以为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
20.下列式子计算正确的是( )
| A. | (-1)-1=1 | B. | (π-3.14)0=0 | C. | 24÷26=22 | D. | ${({-\frac{1}{2}})^{-3}}$=-8 |
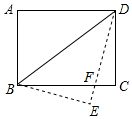 如图,在矩形ABCD中,AB=6,BC=8,将矩形纸片沿BD折叠,使点A落在点E处,设DE与BC相交于点F,则BF的长为$\frac{25}{4}$.
如图,在矩形ABCD中,AB=6,BC=8,将矩形纸片沿BD折叠,使点A落在点E处,设DE与BC相交于点F,则BF的长为$\frac{25}{4}$.